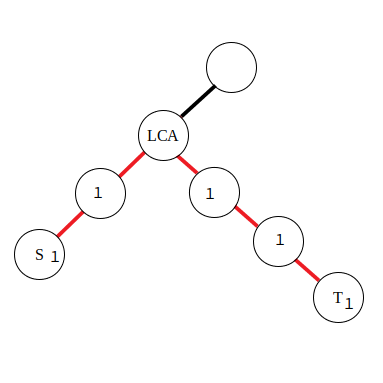
树上前缀和
当题目多次询问树上的一些路径的权值之和,此时可以考虑使用树上前缀和。这里所说的树上的路径可以类比为一维序列的区间。
树上前缀和分为点前缀和和边前缀和。
设
- 点权:
路径上的和为: - 边权:
路径上的和为:
树上差分
树上差分是对树上的某一段路径进行差分操作,这里所说的路径可以类比为一维数组的区间。树上差分常用在题目要求对树上的一些路径进行加法操作,之后询问某条边或某个点经过操作后的值。
树上差分分为点差分和边差分。
点差分
点差分要解决的问题是将树上
设
之后可使用 DFS 计算任意节点的权值(该节点权值等于其本身及其所有子节点的权值之和)。
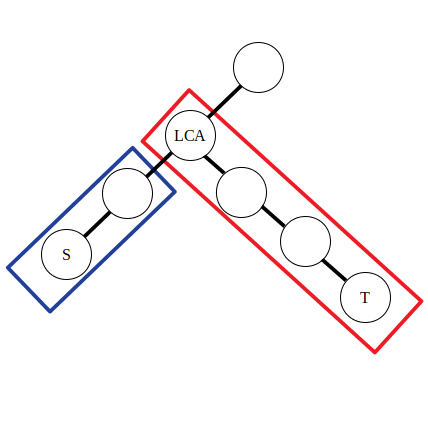
边差分
边差分要解决的问题是将树上
设