问题引入

洛谷 P2495.【SDOI】2011消耗战

题目大意：有 $n$ 个点 $n-1$ 条边的树，根结点为 $1$ 号点，每次询问给定 $k$ 个节点，你可以破坏任意条边，每条边均有不同的代价，问使得这 $k$ 个节点不与根结点联通的最小代价。

朴素做法的时间复杂度为 $O(nk)$，可以直接跑树形DP。

但是不难发现树中的很多节点其实是无用的，因此这启发我们浓缩信息，把整棵大树浓缩成一颗小树。

虚树

抽离查询点和他们两两之间的最近公共祖先以及树根而构成的树，称为虚树。

构成虚树的点称为关键点，关键点 = 查询点 + 两两之间的最近公共祖先 + 树根。

虚树的大小：如果有 $k$ 个查询点，则构成虚树的关键点最多不超过 $2\times k$。例如选择满二叉树的所有叶子节点作为查询点，则虚树为原树。

虚树常用于解决一类树形动态规划问题。题目通常是计算树上部分信息，给出多组询问，询问点的总数量有限。

构建虚树

两次排序 + LCA连边

因为多个查询点的 LCA 可能相同，所以我们不能多次将它加入虚树。

因此我们考虑将查询点按 dfs 序排序。遍历一遍，任意两个相邻的查询点之间求 LCA 并判重，然后根据原树中的祖先后代关系建树。

具体操作为，在查询点的 dfs 序中，枚举相邻的两个数，求得 lca 之后加入序列 $A$ 中，因为 dfs 序的性质，此时的序列 $A$ 已经包含了虚树中的所有点，但是可能存在重复。

所以我们把序列 $A$ 按 dfs 序从小到达排序去重。

最后在序列 A 上，枚举相邻的两个点的编号 $(x,y)$，求得 $lca(x,y)$ 并连接 $lca(x,y)$ 与 $y$，虚树就构造完成了。

int dfn[N], key[N], A[N], cnt;

bool cmp(int x, int y) {
    return dfn[x] < dfn[y];
}

void build() {
    sort(key + 1, key + k + 1, cmp); // 把查询点按 dfs 序排序
    for (int i = 1; i < m; i++) {
        A[++cnt] = key[i];
        A[++cnt] = lca(key[i], key[i + 1]);
    }
    A[++cnt] = key[k];
    sort(A + 1, A + cnt + 1, cmp); // 把虚树上的点按 dfs 序排序
    cnt = unique(A + 1, A + cnt + 1) - A - 1; // 去重
    for (int i = 1; i < cnt; i++) {
        int t = lca(A[i], A[i + 1]);
        add(t, A[i + 1]); // 连边
    }
}

单调栈

1. 先预处理原树的 lca 和 dfs 序，然后用单调栈维护关键点，构造虚树。

2. 对 $k$ 个查询点按 dfs 序排序，先加入跟节点，再按顺序加入查询点。

3. 单调栈维护从根向下的一条链上的关键点，按深度从小到大存储。当单调栈中加入 $a_x$ 后满足 $s_1=root,s_{top}=a_x,fa(s_x)=s_{x-1}$。

4. 当虚树中加入查询点 $a_i$ 时，设 $lca=LCA(s_{top},a_i)$，分类讨论：

   1. $lca=s_{top}$，即 $a_i$ 是 $s_{top}$ 子树内的节点，直接把 $a_i$ 入栈。
   2. $lca\ne s_{top}$，即 $a_i$ 不是 $s_{top}$ 子树内的节点。$lca$ 下面路径上的关键点都应该出栈，出栈时从 $s_{top-1}$ 向 $s_{top}$ 连边，

   注意：当 $dep[s_{top-1}]\le dep[lca]$ 时，停止出栈，此时：

   1. 如果 $lca=s_{top}$，说明 $lca$ 已在栈中，那么直接把 $a_i$ 入栈。
   2. 如果 $lca\ne s_{top}$，说明 $lca$ 不在栈中，$s_{top}$ 依然在 $lca$ 的下面。先从 $lca$ 向 $s_{top}$ 连边，再把 $s_{top}$ 出栈，把 $lca$ 入栈，把 $a_i$ 入栈。

   枚举结束后，还要把最后一条链上的关键点连边，出栈。

int h[N], e[M], ne[M], idx;
int k, root, key[N], dfn[N], dep[N];
int s[N], top;

bool cmp(int x, int y) {
    return dfn[x] < dfn[y];
}

void build() {
    // 注意，如果使用邻接表请将计数器清零
    idx = 0;

    sort(key + 1, key + k + 1, cmp);

    root = 1, top = 0;
    s[++top] = root; // 根节点入栈
    if (key[1] != root) s[++top] = key[1];

    for (int i = 2; i <= k; i++) { // 枚举查询点
        int lca = LCA(s[top], key[i]);
        // 对当前链连边，top 出栈
        while (top > 1 && dep[s[top - 1]] >= dep[lca]) {
            add(s[top - 1], s[top]); // 连边
            top--;
        }
        // 对 lca 和 top 连边，top 出栈，lca 入栈
        if (lca != s[top]) {
            add(lca, s[top]); // 连边
            s[top] = lca;
        }
        s[++top] = key[i]; // 查询点入栈
    }

    while (top) {
        add(s[top - 1], s[top]);
        top--; 
    }
}

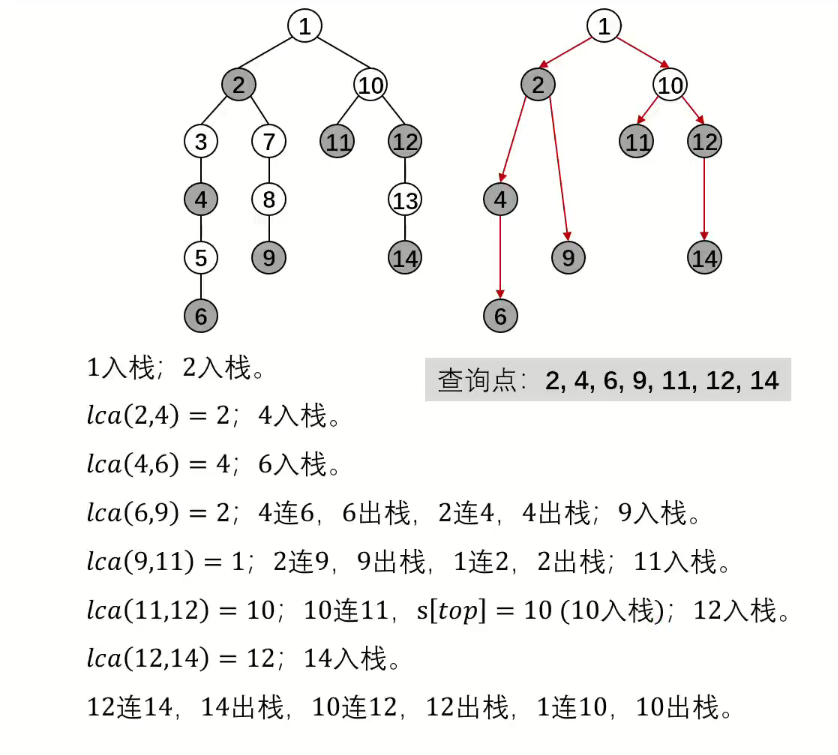
示例如下：