二叉搜索树与平衡树基础
对于二叉树有两个比较重要的基础性质:
- 堆性质
BST性质
BST
给定一颗二叉树,树上每个节点都带有权值(也成为关键码),对于树中任意一个节点都满足 BST 性质,即:
- 该节点的关键码不小于它的左子树中任意节点的关键码;
- 该节点的关键码不大于它的右子树中任意节点的关键码;
则称该树为二叉搜索树(Binary Search Tree,BST)。显然,二叉搜索树的中序遍历是一个关键码单调递增的序列。
BST 的实现
为了方便,我们一般习惯于在 BST 中额外插入一个关键码为 INF 和一个关键码为 -INF 的哨兵节点,这样就可以方便地处理一些边界情况。
注意:以下描述中我们假设 BST 中不存在关键码相同的节点!
// 建立 BST
struct BST {
int l, r, val;
} tr[N];
int tot, root, INF = 0x7f7f7f7f;
int newNode(int val) {
tr[++tot].val = val;
return tot;
}
void build() {
newNode(-INF), newNode(INF);
root = 1;
tr[1].r = 2;
}
// 注意以下操作中均以根节点开始,即 `p = root`
// 检索 BST 中是否存在 val
int search(int p, int val) {
if (p == 0) return 0; // 检索失败
if (val == tr[p].val) return p; // 检索成功
return search(val < tr[p].val? tr[p].l : tr[p].r, val); // 递归搜索左右子树
}
// 插入 val 到 BST 中
void insert(int &p, int val) {
if (p == 0) {
// 需要注意的是这里的 p 是引用,其父节点的 l 或 r 的值会被同时更新
p = newNode(val);
return ;
}
if (val == tr[p].val) return ; // 关键码相同,不插入
if (val < tr[p].val) insert(tr[p].l, val); // 插入到左子树
else insert(tr[p].r, val); // 插入到右子树
}
// 求 BST 中 val 的前驱/后继,以后继为例,前驱同理
int getNext(int val) {
int ans = 2;
int p = root;
while (p) {
if (val == tr[p].val) { // val 存在
if (tr[p].r > 0) { // 有右子树
p = tr[p].r;
// 右子树一直往左走
while (tr[p].l > 0) p = tr[p].l;
ans = p;
}
break;
}
// 对于经过的每一个节点都尝试更新 ans
if (val < tr[p].val && tr[p].val < tr[ans].val) ans = p;
p = val < tr[p].val ? tr[p].l : tr[p].r;
}
return ans;
}
// 删除 BST 中 val
void remove(int val) {
int &p = root;
while (p) {
if (val == tr[p].val) break;
p = val < tr[p].val ? tr[p].l : tr[p].r;
}
if (p == 0) return ; // val 不存在
if (tr[p].l == 0) {
// 没有左子树,直接用右子树替换掉 p
p = tr[p].r;
} else if (tr[p].r == 0) {
// 没有右子树,直接用左子树替换掉 p
p = tr[p].l;
} else {
// 有左右子树,找到右子树中最小的节点替换掉 p
int next = tr[p].r;
while (tr[next].l > 0) next = tr[next].l;
// next 一定没有左子树,直接删除即可
remove(tr[next].val);
// 令节点 next 替代节点 p 的位置
tr[next].l = tr[p].l, tr[next].r = tr[p].r;
p = next;
}
}BST 存在的一些问题
在随机数据中,BST 一次操作的期望复杂度是 BST 很容易退化!例如如果我们在 BST 中插入一个有序序列,那么 BST 就会变成一条链,此时,BST 的操作复杂度就退化成
对于这种左右子树相差很大的 BST 我们称其为是“不平衡”的!平衡的定义有很多,比如:
- 左右子树的高度差不超过
; - 左右子树的节点数差不超过
;
对平衡的定义的不同,由此引申出了许多不同的平衡树,如 Treap、AVL 树、Splay、红黑树等。
下面我们介绍一种入门级的平衡树:Treap。
Treap
满足 BST 性质且中序遍历序列相同的二叉搜索树是不唯一的,如果我们可以改变二叉搜索树的形态,使其达到平衡状态,且不影响其 BST 性质,那么我们就可以得到一个平衡的 BST 树。
改变形态并保持 BST 性质的操作有很多,其中最常见的就是 旋转 操作。最基本的旋转操作称为单旋转,它又分为左旋和右旋,如图:
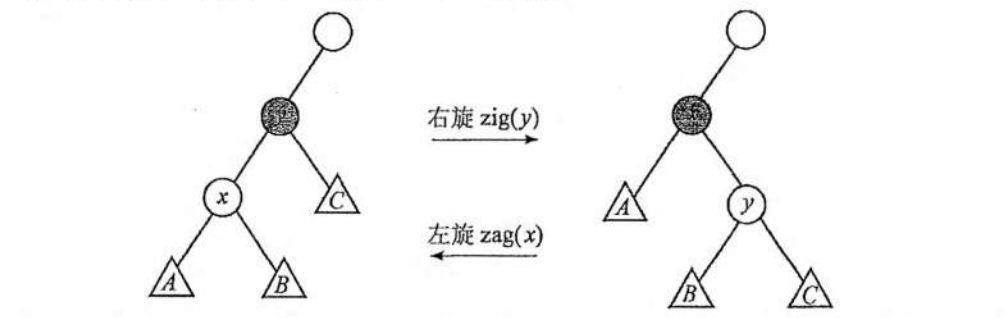
右旋:将 p 节点的左子节点绕着 p 向右旋转,即将 p 的左子节点变为 p 的父亲,p 作为 p 的左子节点(此时该节点是 p 的父亲)的右子节点,p 的左子节点(此时该节点是 p 的父亲)的右子树作为 p 的左子树。
void zig(int &p) {
int q = tr[p].l;
tr[p].l = tr[q].r, tr[q].r = p, p = q;
}左旋:将 p 节点的右子节点绕着 p 向左旋转,即将 p 的右子节点变为 p 的父亲,p 作为 p 的右子节点(此时该节点是 p 的父亲)的左子节点,p 的右子节点(此时该节点是 p 的父亲)的左子树作为 p 的右子树。
void zag(int &p) {
int q = tr[p].r;
tr[p].r = tr[q].l, tr[q].l = p, p = q;
}为了制造旋转,以使 BST 树尽可能平衡,我们引入了一个随机优先级,使其满足堆性质,当插入或是删除时,我们可以根据随机优先级是否满足堆性质制造旋转,调整 BST 树的平衡。这就是 Treap。
Treap 的实现
Treap = Tree + Heap,即树和堆的结合。Treap 是一个二叉搜索树,其每个节点除关键码(满足 BST 性质)外都额外带有一个随机权值 dat(满足大根堆性质),用于实现 Treap 树的平衡性。
注意:Treap 不能保证每次生成的 Treap 树都是平衡的,但它保证了 Treap 树的期望高度是
参见例题:
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
struct Treap {
int l, r;
int val, dat; // 关键码 优先级
int cnt, size; // 节点计数 子树大小
} tr[N];
int tot, root, n, INF = 0x7fffffff;
int newNode(int val) {
tr[++tot].val = val;
tr[tot].dat = rand();
tr[tot].cnt = tr[tot].size = 1;
return tot;
}
void pushup(int p) {
tr[p].size = tr[tr[p].l].size + tr[tr[p].r].size + tr[p].cnt;
}
void build() {
newNode(-INF), newNode(INF);
root = 1;
tr[1].r = 2;
pushup(root);
}
int getRankByVal(int p, int val) {
if (p == 0) return 0;
if (val == tr[p].val) return tr[tr[p].l].size + 1;
if (val < tr[p].val) return getRankByVal(tr[p].l, val);
return getRankByVal(tr[p].r, val) + tr[tr[p].l].size + tr[p].cnt;
}
int getValByRank(int p, int rank) {
if (p == 0) return INF;
if (tr[tr[p].l].size >= rank) return getValByRank(tr[p].l, rank);
if (tr[tr[p].l].size + tr[p].cnt >= rank) return tr[p].val;
return getValByRank(tr[p].r, rank - tr[tr[p].l].size - tr[p].cnt);
}
void zig(int &p) {
int q = tr[p].l;
tr[p].l = tr[q].r, tr[q].r = p, p = q;
pushup(tr[p].r), pushup(p);
}
void zag(int &p) {
int q = tr[p].r;
tr[p].r = tr[q].l, tr[q].l = p, p = q;
pushup(tr[p].l), pushup(p);
}
void insert(int &p, int val) {
if (p == 0) {
p = newNode(val);
return ;
}
if (val == tr[p].val) {
tr[p].cnt++;
pushup(p);
return ;
}
if (val < tr[p].val) {
insert(tr[p].l, val);
if (tr[p].dat < tr[tr[p].l].dat) zig(p);
} else {
insert(tr[p].r, val);
if (tr[p].dat < tr[tr[p].r].dat) zag(p);
}
pushup(p);
}
int getPre(int val) {
int ans = 1;
int p = root;
while (p) {
if (val == tr[p].val) {
if (tr[p].l > 0) {
p = tr[p].l;
while (tr[p].r > 0) p = tr[p].r;
ans = p;
}
break;
}
if (tr[p].val < val && tr[p].val > tr[ans].val) ans = p;
p = val < tr[p].val ? tr[p].l : tr[p].r;
}
return tr[ans].val;
}
int getNext(int val) {
int ans = 2;
int p = root;
while (p) {
if (val == tr[p].val) {
if (tr[p].r > 0) {
p = tr[p].r;
while (tr[p].l > 0) p = tr[p].l;
ans = p;
}
break;
}
if (tr[p].val > val && tr[p].val < tr[ans].val) ans = p;
p = val < tr[p].val ? tr[p].l : tr[p].r;
}
return tr[ans].val;
}
void remove(int &p, int val) {
if (p == 0) return ;
if (val == tr[p].val) {
if (tr[p].cnt > 1) {
tr[p].cnt --;
pushup(p);
return ;
}
if (tr[p].l || tr[p].r) {
if (tr[p].r == 0 || tr[tr[p].l].dat > tr[tr[p].r].dat) {
zig(p), remove(tr[p].r, val);
} else {
zag(p), remove(tr[p].l, val);
}
pushup(p);
} else {
p = 0;
}
return ;
}
val < tr[p].val ? remove(tr[p].l, val) : remove(tr[p].r, val);
pushup(p);
}
int main() {
build();
cin >> n;
while (n--) {
int opt, x; cin >> opt >> x;
if (opt == 1) insert(root, x);
else if (opt == 2) remove(root, x);
else if (opt == 3) cout << getRankByVal(root, x) - 1 << endl;
else if (opt == 4) cout << getValByRank(root, x + 1) << endl;
else if (opt == 5) cout << getPre(x) << endl;
else cout << getNext(x) << endl;
}
return 0;
}