FHQ Treap
FHQ Treap 又称无旋 Treap,它抛弃了传统的旋转操作,转而使用分裂和合并两个操作来维护树平衡。它的性能与 Splay 相当,代码量却比 Splay 少很多,非常适合竞赛使用!
它的两个基本操作:
- 分裂:按权值
val进行分裂 - 合并:按随机值
key进行合并
分裂操作
分裂函数:void split(int p, int v, int &x, int &y);
它的含义是:
- 将树
p按值v分裂成两颗子树:左子树x和右子树y。 - 分裂后的子树
x中的权值都不大于v,子树y中的权值都大于v。
void split(int p, int v, int &x, int &y) {
if (!p) {
x = y = 0;
return;
}
if (tr[p].val <= v) {
// 把 x 指向左 Treap 的根
x = p;
// 递归分裂右子树
split(tr[p].r, v, tr[p].r, y);
} else {
y = p;
split(tr[p].l, v, x, tr[p].l);
}
pushup(p);
}这里我们分析代码中的第一种情况,第二种情况类似。如果当前节点 p 的 val 值小于等于给定值 v,说明 p 以及其左子树都小于 v,应属于分裂后的左 Treap,p 的右子树也可能部分小于等于 v,因此需要继续递归分裂右子树,把小于等于 v 的那部分作为 p 的右子树。把 x 指向左 Treap 的根。
如图:
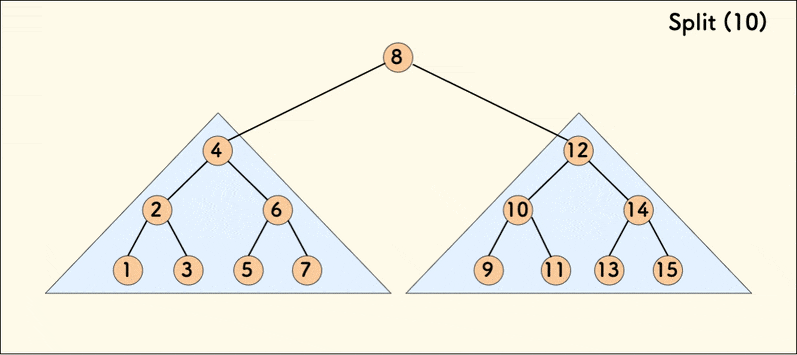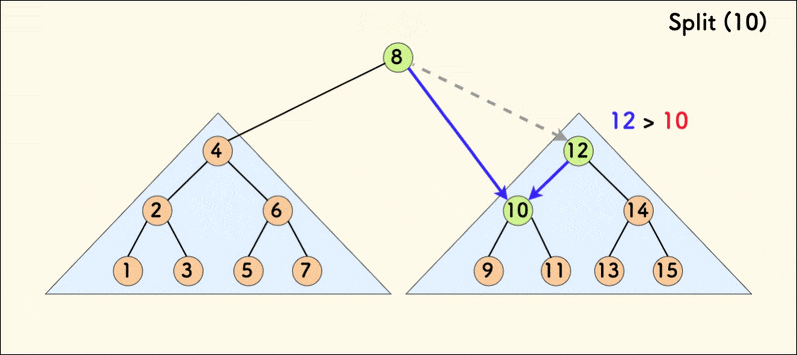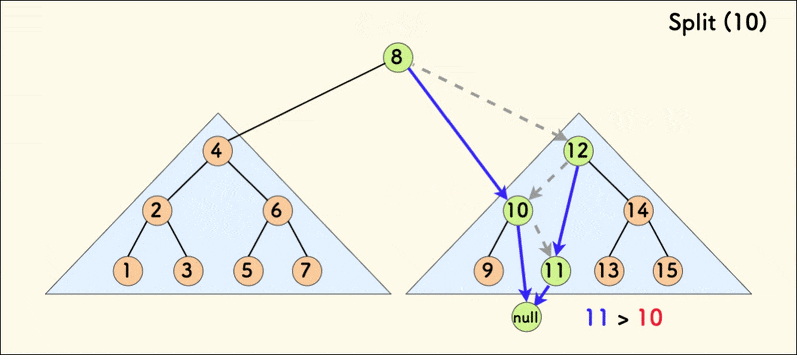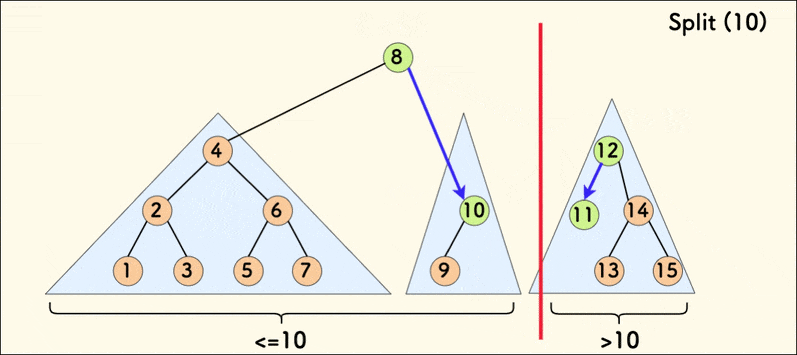
显然我们发现分裂操作仅利用了二叉搜索树的性质,且不改变中序遍历序列。
具体示例:
graph TD;
6((6));
2((2));
8((8));
1((1));
5((5));
5`((5`));
3((3));
3`((3`));
4((4));
6-.-2;
6---8;
2---1;
2-.-5;
5-.-3;
5---5`;
3---3`;
3-.-4;函数调用流程:
p = 6, v = 3
split(6, 3, x, y)
y = 6
split(2, 3, x, tr[6].l)
pushup(6)
split(2, 3, x, tr[6].l)
x = 2
split(5, 3, tr[2].r, tr[6].l)
pushup(2)
split(5, 3, tr[2].r, tr[6].l)
y = tr[6].l = 5
split(3, 3, tr[2].r, tr[5].l)
pushup(5)
split(3, 3, tr[2].r, tr[5].l)
x = tr[2].r = 3
split(4, 3, tr[3].r, tr[5].l)
pushup(3)
split(4, 3, tr[3].r, tr[5].l)
y = tr[5].l = 4
split(0, 3, tr[3].r, tr[4].l)
pushup(4)
split(0, 3, tr[3].r, tr[4].l)
tr[3].r = tr[4].l = 0合并操作
合并函数:int merge(int x, int y);
它的含义是:
- 将
x和y两颗Treap按随机值key合并成一颗Treap,其中key值小的在上(小根堆)。 - 合并前
x中节点的权值都小于y中节点的权值。
显然,split 分裂后产生的两颗子树是满足 merge 的要求的。
int merge(int x, int y) {
if (!x || !y) return x + y;
if (tr[x].key < tr[y].key) {
// 递归合并 x.r 与 y
// y` 成为 x 新的右子树
tr[x].r = merge(tr[x].r, y);
pushup(x);
return x;
} else {
tr[y].l = merge(x, tr[y].l);
pushup(y);
return y;
}
}这里我们分析代码中的第一种情况,第二种情况类似。如果 x 的 key 值小于 y 的 key 值,那么应该把 x 节点作为新树的根,同时因为 x 中的节点权值都小于 y 中的节点权值,所以要把 y 放在新树的右子树中(先把 x 原来的右子树 x.r 与 y 合并,得到的新树即是 x 新的右子树)。
如图:
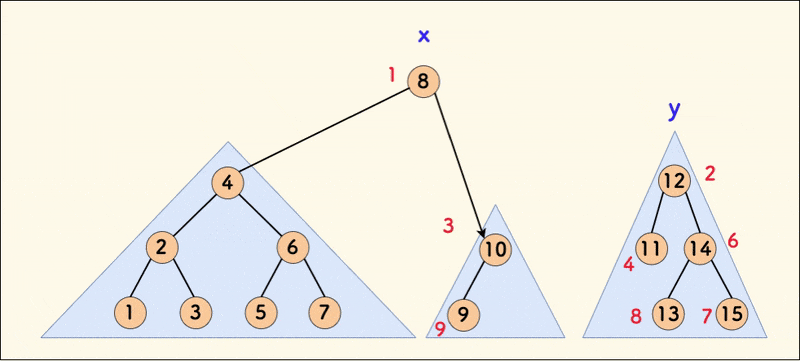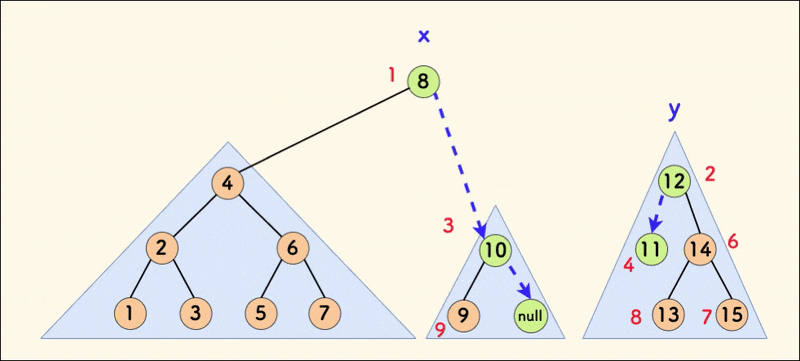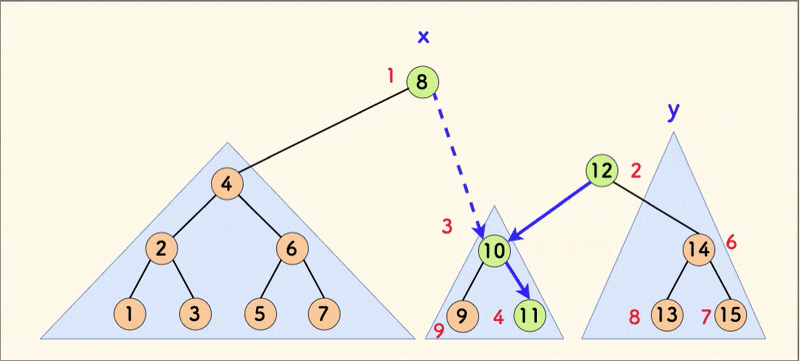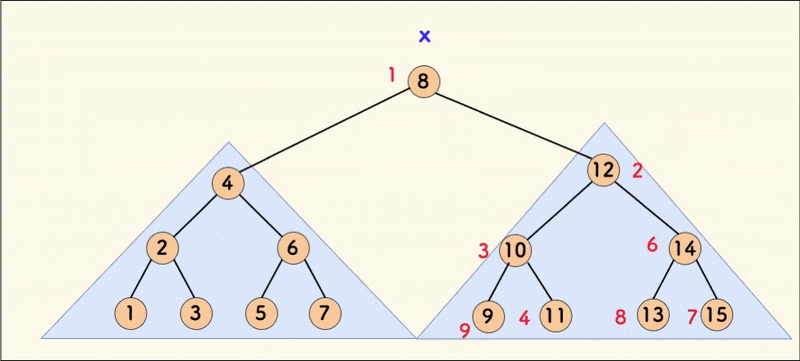
合并操作保证了堆性质,从而让树尽可能保持平衡,且其不改变中序遍历序列
具体示例:
graph TD;
6((6,1));
2((2,2));
8((8,3));
1((1,4));
5((5,4));
5`((5`,6));
3((3,5));
3`((3`,7));
4((4,8));
6-.-5;
6---8;
5-.-4;
5---5`;
2---1;
2-.-3;
3---3`;函数调用流程:
x = 2, y = 6
merge(2, 6)
tr[6].l = merge(2, 5)
pushup(6)
return 6
merge(2, 5)
tr[2].r = merge(3, 5)
pushup(2)
return 2
merge(3, 5)
tr[5].l = merge(3, 4)
pushup(5)
return 5
merge(3, 4)
tr[3].r = merge(0, 4)
pushup(3)
return 3
merge(0, 4)
return 4代码实现
以本题为例:洛谷 P3368. 普通平衡树
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
struct {
int l, r;
int val, key;
int sz;
} tr[N];
int tot, root, n;
int newNode(int v) {
tr[++tot].val = v;
tr[tot].key = rand();
tr[tot].sz = 1;
return tot;
}
void pushup(int p) {
tr[p].sz = tr[tr[p].l].sz + tr[tr[p].r].sz + 1;
}
void split(int p, int v, int &x, int &y) {
if (!p) {
x = y = 0;
return;
}
if (tr[p].val <= v) {
x = p;
split(tr[p].r, v, tr[p].r, y);
} else {
y = p;
split(tr[p].l, v, x, tr[p].l);
}
pushup(p);
}
int merge(int x, int y) {
if (!x || !y) return x + y;
if (tr[x].key < tr[y].key) {
tr[x].r = merge(tr[x].r, y);
pushup(x);
return x;
} else {
tr[y].l = merge(x, tr[y].l);
pushup(y);
return y;
}
}
// 插入一个权值为 v 的新节点
void insert(int v) {
// 按 v 进行分裂,从而找到插入位置
int x, y, z;
split(root, v, x, y);
// 新建节点
z = newNode(v);
// 依次合并 x、z、y
root = merge(merge(x, z), y);
}
// 删除权值为 v 的节点
void remove(int v) {
int x, y, z;
// 按 v 进行分裂 x <= v < z
split(root, v, x, z);
// 再按 v - 1 进行分裂 x <= v - 1 < y <= v
split(x, v - 1, x, y);
// 此时 y 即是待删除节点,合并其左右子树
y = merge(tr[y].l, tr[y].r);
// 再依次合并 x、y、z
root = merge(merge(x, y), z);
}
// 求权值为 v 的节点排名
int getRankByVal(int v) {
int x, y;
split(root, v - 1, x, y);
int ans = tr[x].sz + 1;
root = merge(x, y);
return ans;
}
// 求排名为 k 的节点的值
int getValByRank(int p, int k) {
if (k <= tr[tr[p].l].sz) return getValByRank(tr[p].l, k);
else if (k == tr[tr[p].l].sz + 1) return tr[p].val;
else return getValByRank(tr[p].r, k - tr[tr[p].l].sz - 1);
}
// 求 v 前驱节点
int getPre(int v) {
int x, y;
split(root, v - 1, x, y);
int ans = getValByRank(x, tr[x].sz);
root = merge(x, y);
return ans;
}
// 求 x 后继节点
int getNext(int v) {
int x, y;
split(root, v, x, y);
int ans = getValByRank(y, 1);
root = merge(x, y);
return ans;
}
int main() {
cin >> n;
while (n--) {
int opt, x; cin >> opt >> x;
if (opt == 1) insert(x);
else if (opt == 2) remove(x);
else if (opt == 3) cout << getRankByVal(x) << endl;
else if (opt == 4) cout << getValByRank(root, x) << endl;
else if (opt == 5) cout << getPre(x) << endl;
else cout << getNext(x) << endl;
}
return 0;
}FHQ Treap 的区间操作
支持区间操作的 FHQ Treap 相较于普通的 FHQ Treap 区别主要在于分裂函数由原来的按值分裂改为了现在的按位置分裂,同时实现区间更新时,引入了延迟标记机制。
何为按位置分裂
原来的 FHQ Treap 是对权值构建的二叉搜索树,现在我们改为按权值下标构建二叉搜索树,抛弃随机优先级,使权值满足堆性质。
由于下标天生严格有序,所以对下标的中序遍历就是下标的递增序列。无论分裂还是合并操作,都不会改变下标的顺序。
此时的 FHQ Treap 可以类比线段树,看作区间树:
- 每个节点代表原数组的一个区间。
- 父节点的区间 = 左子树区间 + 右子树区间 + 父节点本身。
- 对于任意区间,都可以分裂出一颗子树表示。
代码实现
以本题为例:洛谷 P3391: 文艺平衡树
const int N = 1e5 + 10;
struct {
int l, r;
int val, key;
int sz;
int tag; // 延迟标记
} tr[N];
int tot, root, n;
int newNode(int v) {
// 注意这里的 val 值是下标
tr[++tot].val = v;
// 注意这里的 key 值是权值,可传入具体值取代随机值
tr[tot].key = rand();
tr[tot].sz = 1;
return tot;
}
void pushup(int p) {
tr[p].sz = tr[tr[p].l].sz + tr[tr[p].r].sz + 1;
}
void pushdown(int p) {
if (tr[p].tag) {
swap(tr[p].l, tr[p].r);
tr[tr[p].l].tag ^= 1;
tr[tr[p].r].tag ^= 1;
tr[p].tag = 0;
}
}分裂操作
void split(int p, int k, int &x, int &y);
它的含义是:
- 在位置
k处分裂p为两颗子树:左子树x和右子树y。 - 分裂后的子树
x中的下标都不大于k,子树y中的下标都大于k。
void split(int p, int k, int &x, int &y) {
if (!p) {
x = y = 0;
return ;
}
pushdown(p);
if (k > tr[tr[p].l].sz) {
k -= tr[tr[p].l].sz + 1;
x = p;
split(tr[p].r, k, tr[p].r, y);
} else {
y = p;
split(tr[p].l, k, x, tr[p].l);
}
pushup(p);
}剖分区间 $[l, r]:先分裂出区间
int x, y, z;
split(root, r, x, z);
split(x, l - 1, x, y);合并操作
合并操作的几无变化,主要是添加了两次 pushdown 操作。
int merge(int x, int y) {
if (!x || !y) return x + y;
if (tr[x].key < tr[y].key) {
pushdown(x); // pushdown 左子树
tr[x].r = merge(tr[x].r, y);
pushup(x);
return x;
} else {
pushdown(y); // pushdown 右子树
tr[y].l = merge(x, tr[y].l);
pushup(y);
return y;
}
}区间操作
对于本题我们还需要解决两个问题,区间翻转和输出结果。
void reverse(int l, int r) {
int x, y, z;
split(root, r, x, z);
split(x, l - 1, x, y);
tr[y].tag ^= 1; //标记
root = merge(merge(x, y), z);
}
void print(int p) {
if (!p) return ;
pushdown(p);
print(tr[p].l);
cout << tr[p].val << " ";
print(tr[p].r);
}