何为笛卡尔树
笛卡尔树是一种特殊的、简化的 Treap 树。它的每一个节点由一个键值二元组 BST 性质),而
如图:
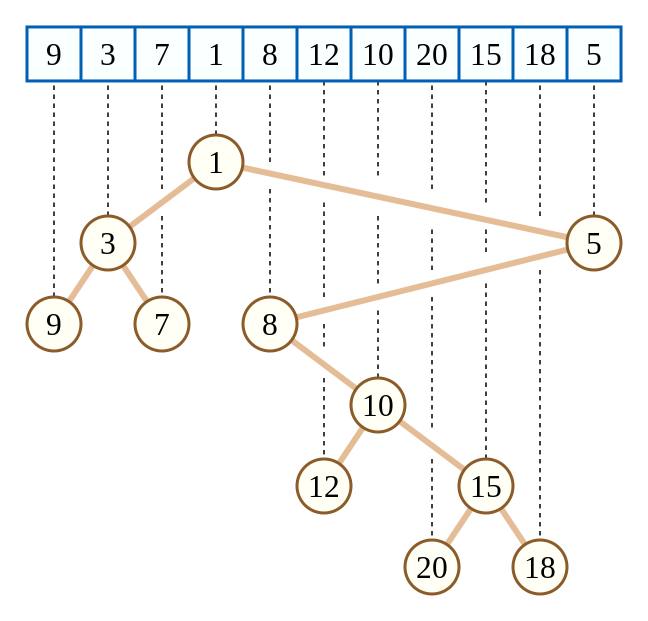
笛卡尔树的构建
考虑将元素按下标顺序依次插入到当前的笛卡尔树中,那么每次插入的元素必然在这棵树的最右链的末端,为此我们可以使用单调栈维护最右链,时间复杂度为
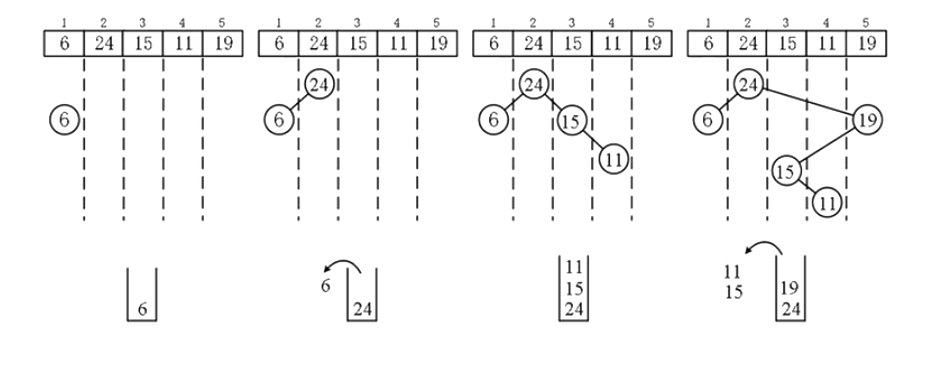
cpp
// 以大根堆为例
for (int i = 1; i <= n; i++) {
int k = top;
while (k > 0 && v[st[k]] < v[i]) k--;
if (k) rs[st[k]] = i; // 栈顶元素的右儿子 = 当前元素
if (k < top) ls[i] = st[k + 1]; // 当前元素的左儿子 = 上一个被弹出的元素
st[++k] = i; // 当前元素入栈
top = k;
}笛卡尔树的应用
笛卡尔树的直接应用是求解 RMQ 问题,即求区间 LCA 所在节点即可。
