线段树

线段树是一种基于分治思想的二叉树，用于在区间上进行信息统计。包括单点修改、区间修改、区间查询（区间求和、区间最大值、区间最小值）。时间复杂度为 $O(logn)$。

线段树的定义

1. 线段树的每个节点都代表一个区间。
2. 线段树具有唯一根节点，代表整个统计区间。
3. 线段树的每个叶子节点都代表一个长度为 $1$ 的区间。
4. 对于每个内部节点 $[l,r]$，它的左右子节点分别代表区间 $[l,mid]$ 和 $[mid+1,r]$，其中 $mid=\lfloor \frac{l+r}{2}\rfloor$。

如图：

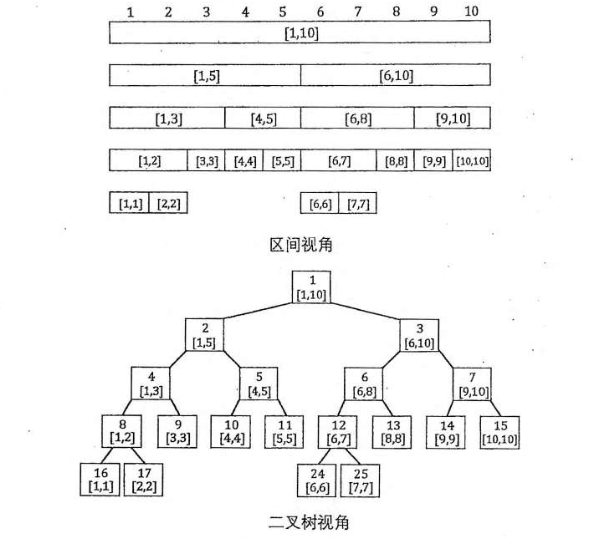
注意：保存线段树的数组长度为 $4N$，其中 $N$ 为序列长度。

关于线段树的空间消耗：$n$ 个叶子节点的满二叉树有 $n+\frac{n}{2}+\frac{n}{4}+...+1=2n-1$ 个节点，因为最后一层可能会产生空余，所以保存线段树的数组长度不得小于 $4n$。

线段树的操作

以区间最大值问题为例：

线段树的结构：

const int N = 1e5 + 10;

struct SegmentTree {
    int l, r, dat;
} t[N * 4];

void pushup(int p) {
    t[p].dat = max(t[p << 1].dat, t[p << 1 | 1].dat);
}

建树

// 构建线段树，调用入口 build(1, 1, n);
void build(int p, int l, int r) {
    t[p].l = l, t[p].r = r; // 节点 p 代表区间 [l, r]
    if (l == r) {           // 叶子节点
        t[p].dat = a[l];
        return;
    }
    int mid = (l + r) >> 1;
    build(p << 1, l, mid);         // 构造左子树 [l, mid]
    build(p << 1 | 1, mid + 1, r); // 构造右子树 [mid + 1, r]
    pushup(p); // 自下而上传递信息
}

单点修改

单点修改指令形如：C x v，表示把序列 $a[x]$ 的值更改为 $v$。

// 单点修改，把 a[x] 的值更改为 v，调用入口 modify(1, x, v);
void modify(int p, int x, int v) {
    if (t[p].l == x && t[p].r == x) { 	// 找到 x 对应的叶子节点
        t[p].dat = v;
        return;
    }
    int mid = (t[p].l + t[p].r) >> 1;
    if (x <= mid) modify(p << 1, x, v);	// x 在左子树
    else modify(p << 1 | 1, x, v); 		// x 在右子树
    pushup(p); // 自下而上传递信息
}

区间查询

区间查询指令形如：Q l r，表示查询序列 $a$ 在区间 $[l,r]$ 上的最大值。

// 区间查询，查询序列 a 在区间 [l, r] 上的最大值，调用入口 query(1, l, r);
int query(int p, int l, int r) {
    if (t[p].l >= l && t[p].r <= r) return t[p].dat; 		// 当前区间被完全覆盖
    int mid = (t[p].l + t[p].r) >> 1;
    int ans = -1e9;
    if (l <= mid) ans = max(ans, query(p << 1, l, r));		// 当前区间与左子树有交集
    if (r > mid) ans = max(ans, query(p << 1 | 1, l, r));	// 当前区间与右子树有交集
    return ans;
}

区间修改

如果要修改区间 $[l,r]$，可以暴力枚举区间内的所有节点，依次修改，这样做的时间复杂度无法令人接受，因此我们考虑使用线段树的懒惰标记。

懒惰标记即是通过延迟对节点信息的更改，从而减少可能不必要的操作次数。即我们在执行修改指令时，在满足 $l\le p_l\le p_r\le r$ 时直接返回，只不过在回溯之前向节点 $p$ 添加一个标记，表示该节点曾经被修改，但其子节点尚未被更新。如果在后续的指令中，需要从节点 $p$ 向下递归，则需要检查 $p$ 是否有懒惰标记，如果有，则需要更新其子节点，同时为 $p$ 的子节点添加懒惰标记，然后清除 $p$ 的懒惰标记。

以区间求和问题为例：

const int N = 1e5 + 10;

struct SegmentTree {
    int l, r, dat;
    int lazy; // 懒惰标记
} t[N * 4];

void pushup(int p) {
    t[p].dat = t[p << 1].dat + t[p << 1 | 1].dat;
}

void pushdown(int p) {
    if (t[p].lazy) {
        t[p << 1].dat += t[p].lazy * (t[p << 1].r - t[p << 1].l + 1);
        t[p << 1 | 1].dat += t[p].lazy * (t[p << 1 | 1].r - t[p << 1 | 1].l + 1);
        t[p << 1].lazy += t[p].lazy;
        t[p << 1 | 1].lazy += t[p].lazy;
        t[p].lazy = 0;
    }
}

// 区间修改，修改序列 a 在区间 [l, r] 上的值，调用入口 modify(1, l, r, v);
void modify(int p, int l, int r, int v) {
    if (t[p].l >= l && t[p].r <= r) {
        t[p].dat += v * (t[p].r - t[p].l + 1);
        t[p].lazy += v;
        return;
    }

    pushdown(p);

    int mid = (t[p].l + t[p].r) >> 1;
    if (l <= mid) modify(p << 1, l, r, v);
    if (r > mid) modify(p << 1 | 1, l, r, v);
    
    pushup(p);
}

// 带有懒惰标记的区间查询，在裂开时需要下传懒惰标记
int query(int p, int l, int r) {
    if (t[p].l >= l && t[p].r <= r) return t[p].dat;

    pushdown(p); // 下传懒惰标记

    int mid = (t[p].l + t[p].r) >> 1;
    int ans = 0;
    if (l <= mid) ans += query(p << 1, l, r);
    if (r > mid) ans += query(p << 1 | 1, l, r);
    return ans;
}