递推

斐波那契类

1 1 2 3 5 8 13 ...

当前项是前两项元素之和，我们可以使用数组存储中间结果，则 $f[i]=f[i-1]+f[i-2]$ 同时递推的边界条件为 $f[1]=1,f[2]=1$，目标解即为 $f[n]$

同时，为了节省空间，我们可以迭代的来求解：

a = 1;
b = 1;
for (int i = 3; i <= n; i++) {
	t = a + b;
	a = b;
	b = t;
}

cout << b << endl;

通过上面的分析，我们可以看出：递推需要找出前后项之间的关系，确立一个关系式，借助循环语句求解答案。

因此，递推的关键是确定两件事：

1. 递推关系式
2. 递推边界

递推有两种思考方向：

1. 顺推
2. 逆推

经典例题：洛谷 P1255. 数楼梯

$n$ 级台阶，每次可以走 $1$ 级或者 $2$ 级，求不同走法的方案数。

问题分析：当 $n=1、2、3、4、5...$ 时的方案数是多少？斐波那契数列。 $f[i]=f[i-1]+f[i-2]$ 也可以这样理解，当楼梯级数是 $i$ 的方案数是楼梯级数是 $i-1$ 时走 $1$ 级到达第 $i$ 级的方案数加上楼梯级数是 $i-2$ 时走 $2$ 级到达第 $i$ 级的方案数之和。

经典例题：兔子繁殖问题

雌雄兔子各一只放入养殖场中，每只雌兔在出生两个月后每月产雌雄兔子个一只。第 $n$ 个月后养殖场共有多少对兔子？

问题分析：当 $n=1、2、3、4、5...$ 时答案是多少？斐波那契数列。

汉诺塔类

经典例题：求汉诺塔问题中盘子总共移动了多少次？

问题分析：设 $f[i]$ 表示讲 $i$ 个盘子从一个柱子移动到另一个柱子所需要的移动次数。借助递推的思想，可以先整体考虑移动 $A$ 柱上面的 $i-1$ 个盘子到 $B$ 柱，移动次数为 $f[i-1]$，接着将 $A$ 柱上的第 $i$ 个盘子移动到 $C$ 柱上，移动次数为 $1$，最后将 $B$ 柱上的 $i-1$ 个盘子移动到 $C$ 柱上，移动次数为 $f[i-1]$，因此：$f[i]=2\ast f[i-1]+1$，边界条件：$f[1]=1$。

经典例题：Jouier 2410. Strange Towers of Hanoi

问题分析：设 $d[n]$ 表示求解 $n$ 盘 $3$ 塔问题的最少步数，$f[n]$ 表示求解 $n$ 盘 $4$ 塔问题的最少步数。$f[n]=mi{n}_{1\le i<n}\{2\ast f[i]+d[n-i]\}$，边界条件：$f[1]=1$。上式的含义是：先把 $i$ 个盘子在 $4$ 塔模式下移动到 $B$ 柱，然后把 $n-i$ 个盘子在 $3$ 塔模式下移动到 $D$ 柱，最后把 $i$ 个盘子在 $4$ 塔模式下移动到 $D$ 柱。考虑所有可能的 $i$，取最小值即可。

平面分割类

经典例题：设有 $n$ 条封闭曲线画在平面上，而任何两条封闭曲线恰好相交于两点，且任何三条封闭曲线不相交于同一点，问这些封闭曲线把平面分割成的区域个数。

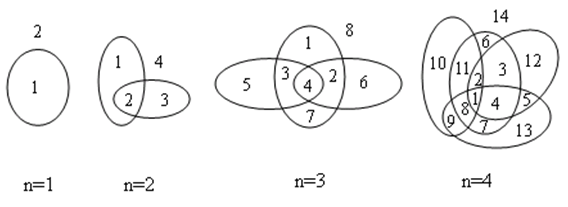
问题分析：当平面上已经有 $n-1$ 条曲线将平面分割成 $f[n-1]$ 个区域后，画第 $n$ 条曲线时，第 $n$ 条曲线与之前 $n-1$ 条曲线每个曲线都会相交，与每个曲线相交会多产生 $2$ 个区域，共多出来 $2\ast (n-1)$ 个区域。$f[n]=f[n-1]+2\ast (n-1)$，边界条件：$f[1]=2$

双递推类

经典例题：位数问题

在所有的 $N$ 位数中，有多少个数中有偶数个数字 $3$？请输出答案对 $12345$ 取余之后的值。

问题分析：设 $f[i][0]$ 表示前 $i$ 位取偶数个 $3$ 有几种情况，$f[i][1]$ 表示前 $i$ 位取奇数个 $3$ 有几种情况。

1. $f[i][0]=f[i-1][0]\ast 9+f[i-1][1]$
2. $f[i][1]=f[i-1][0]+f[i-1][1]\ast 9$
3. 边界条件：$f[1][1]=1,f[1][0]=8$

矩阵递推

经典例题：YBT 1258：数字金字塔

问题分析：设 $f(i,j)$ 表示从 $(1,1)$ 到 $(i,j)$ 的最大路径之和，$f(i,j)=max(f(i-1,j-1),f(i-1,j))+a[i][j]$

边界：$f(1,1)=a[1][1]$

目标解：$max(f(n,j)),1\le j\le n$

以上递推方式为顺推，如何进行逆推呢？请同学们思考！

习题

1. 洛谷 P1002. 过河卒
2. 洛谷 P1044. 栈
3. 洛谷 P1011. 车站
4. 洛谷 P2437. 蜜蜂路线
5. 洛谷 P1164. 小 A 买菜