数组

引入

输入 n 个学生的成绩，输出其平均成绩。

思考：使用 while 循环读入这 n 个学生的成绩，求平均后输出

cin >> n;

float s, sum = 0;
while(scanf("%d", &s) == 1) sum += s;

cout << sum / n << endl;

在上述代码中我们只使用一个变量s就读入了 n 个学生的成绩，但是如果我们要求必须存下这 n 个学生的成绩数据以便不时之需呢？我们该如何存？是定义 n 个变量吗？

何为数组

C++ 支持数组数据结构，它可以存储一个固定大小的相同类型元素的顺序集合。数组是用来存储一系列数据，但它往往被认为是一系列相同类型的变量。

数组的声明并不是声明一个个单独的变量，比如 number0、number1、...、number99，而是声明一个数组变量，比如 numbers，然后使用 numbers[0]、numbers[1]、...、numbers[99] 来代表一个个单独的变量。数组中的特定元素可以通过索引（下标）访问，因此可以说数组是带下标的变量。

所有的数组都是由连续的内存位置组成。最低的地址对应第一个元素，最高的地址对应最后一个元素。

声明数组

在 C++ 中要声明一个数组，需要指定元素的类型和元素的数量，如下所示：

type arrayName [ arraySize ];

这叫做一维数组。arraySize  必须是一个大于零的整数常量，type  可以是任意有效的 C++ 数据类型。

例如：

int score[50];
double names[100];
int n = 10;
int a[n]; // 错误 n不是整形常量
const int N = 10;
int a[N]; // 正确

初始化数组

在 C++ 中，您可以逐个初始化数组，也可以使用一个初始化语句，如下所示：

double balance[5] = {1000.0, 2.0, 3.4, 7.0, 50.0};

大括号 { } 之间的值的数目不能大于我们在数组声明时在方括号 [ ] 中指定的元素数目。

如果您省略掉了数组的大小，数组的大小则为初始化时元素的个数。因此，如果：

double balance[] = {1000.0, 2.0, 3.4, 7.0};

您将创建一个数组，它与前一个实例中所创建的数组是完全相同的。下面是一个为数组中某个元素赋值的实例：

balance[4] = 50.0;

上述的语句把数组中第五个元素的值赋为 50.0。所有的数组都是以 0 作为它们第一个元素的索引，也被称为基索引，数组的最后一个索引是数组的总大小减去 1。以下是上面所讨论的数组的的图形表示：

访问数组元素

数组变量的使用和普通变量是一样的，我们可以通过控制下标来控制某一个数组元素。

int a[10];
// 使用for循环为每一额数组元素赋值
for(int i = 0; i < 10; i++) a[i] = i + 1;

// 操纵数组元素
a[3] = a[1] + a[2];
a[4] = 10;

// 遍历数组
for(int i = 0; i < 10; i++) cout << a[i] << " ";

如果使用下标不当，数组是会发生越界问题的，

数组的操作

插入元素

在数组中插入元素时需要保证数组不溢出

int a[10] = {1, 2, 3, 4, 5, 6, 7,};

// 在下标为k的位置插入元素x
void insert(int x, int k) {
	for(int i = n - 1; i >= k; i--) a[i + 1] = a[i];
	a[k] = x;
	return;
}

删除元素

int a[10] = {1, 2, 3, 4, 5, 6, 7,};

//  删除下标为k的元素
void remove(int k) {
	for(int i = k; i < n; i++) a[i] = a[i + 1];
	return;
}

查找元素

int a[10] = {1, 2, 3, 4, 5, 6, 7,};

// 统计数组中x出现的次数
int find(int x) {
	int cnt = 0;
	for(int i = 0; i < n; i++){
		if(a[i] == x) cnt ++;
	}

	return cnt;
}

数组排序

选择排序

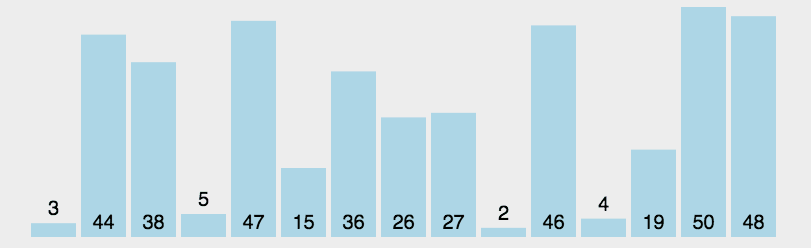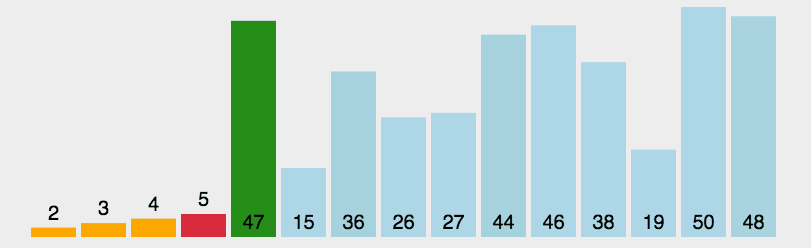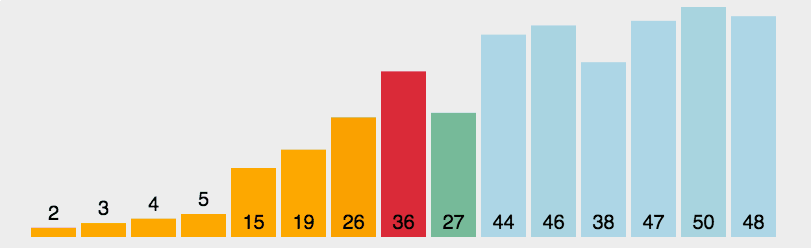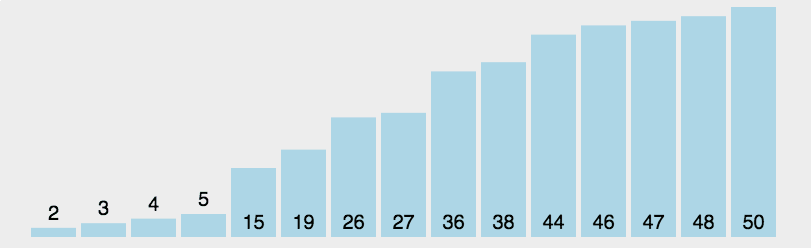
算法描述

1. 在未排序序列中找到最小元素，存放到排序序列的起始位置
2. 从剩余未排序元素中继续寻找最小元素，然后放到已排序序列的末尾。
3. 重复第二步，直到所有元素均排序完毕。

程序模板

void selectSort(int a[]) {
	for(int i = 0; i < n - 1; i++) {
		int k = i;
		for(int j = i + 1; j < n; j++) {
			if(a[k] > a[j]) k = j;
		}

		swap(a[k], a[i]);
	}
}

插入排序

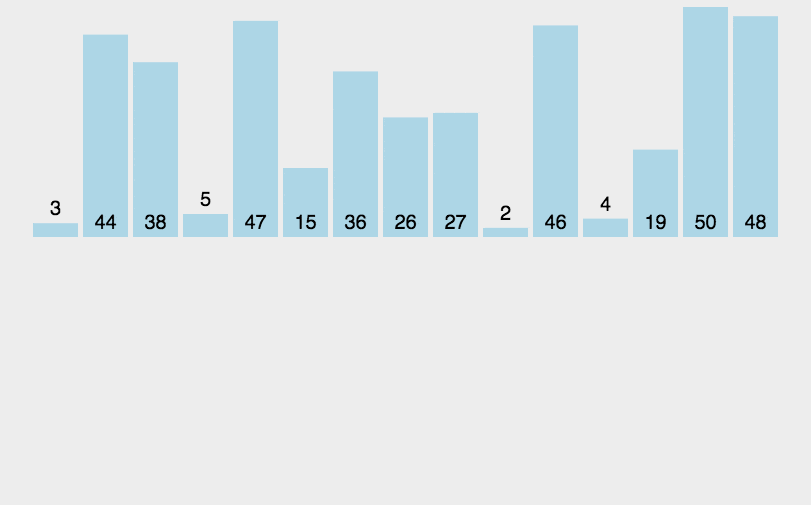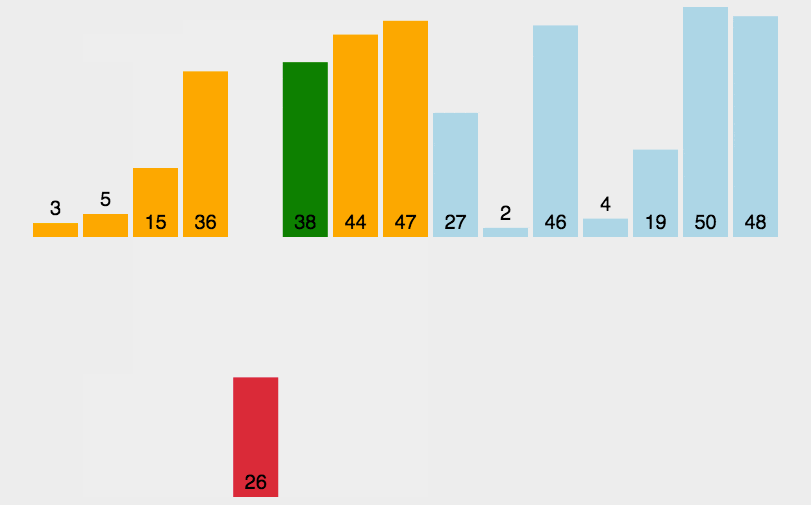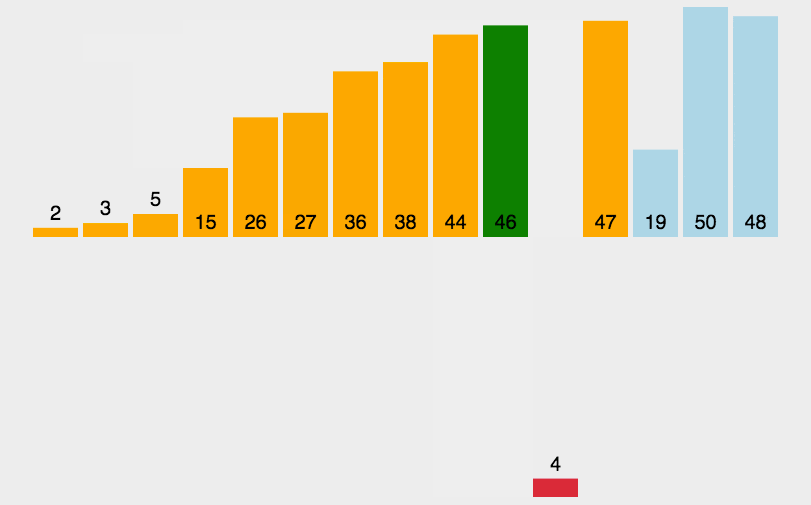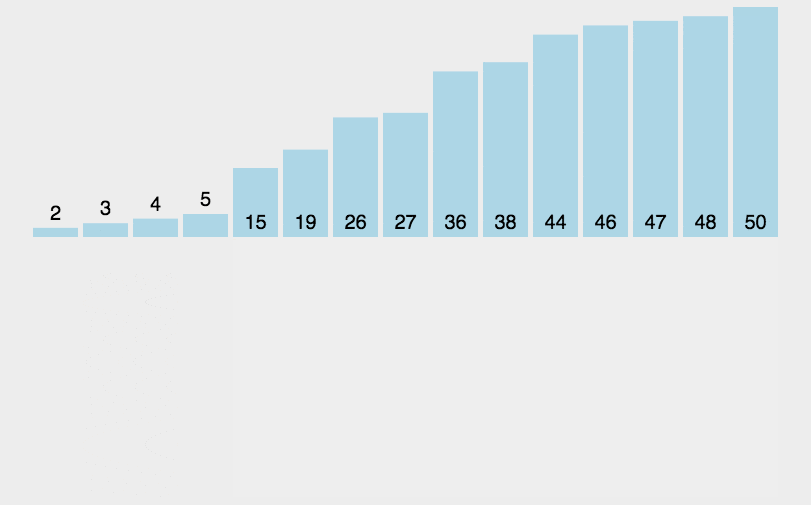
算法描述

1. 从第一个元素开始，该元素可以认为已经被排序
2. 取出下一个元素，在已经排序的元素序列中从后向前扫描
3. 如果该元素（已排序）大于新元素，将该元素移到下一位置
4. 重复步骤 3，直到找到已排序的元素小于或者等于新元素的位置
5. 将新元素插入到该位置后

程序模板

void insertSort(int a[], int n) {
	for(int i = 1; i < n; i++) {
		int j = i - 1;
		int temp = a[i];
		while(j >= 0 && a[j] > temp) {
			a[j + 1] = a[j];
			j--;
		}
		a[j + 1] = temp;
	}
}

冒泡排序

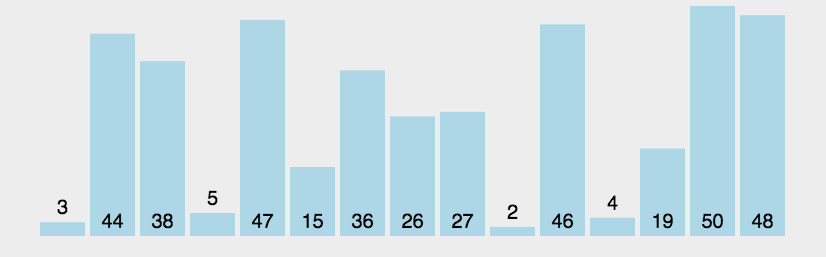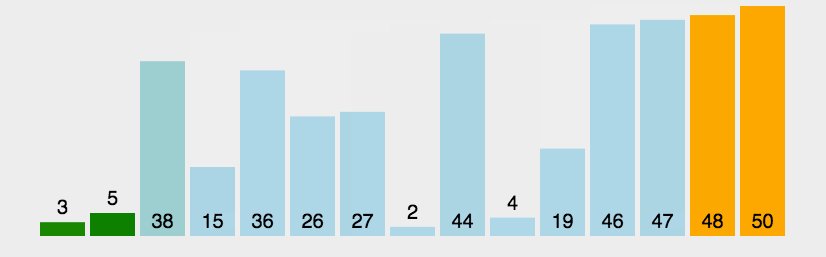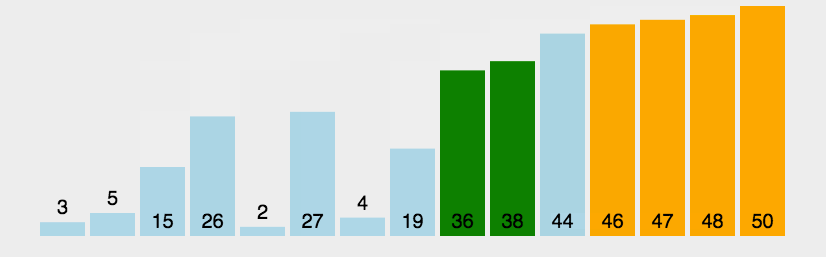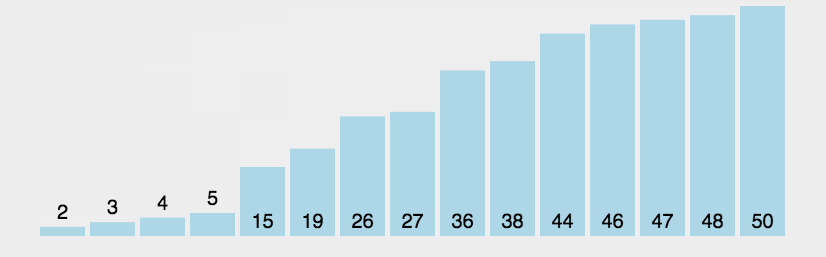
算法描述（向上冒泡）

1. 比较相邻两个元素，大的在后。
2. 从前向后两两比较，一直比较到无序元素的最后两个数据。最终无序元素中最大的数被交换到有序元素的起始的位置。
3. 重复上述过程，直到所有元素有序。

程序模板

void bubbleSort(int a[], int n) {
	bool flag;
	for (int i = 0; i < n - 1; i++) { // 排序 n - 1 趟
		flag = false;
		for (int j = 1; j < n - i; j++) { // n - i 后的已经有序
			if (a[j - 1] > a[j]) {
				swap(a[j - 1], a[j]);
				flag = true;
			}
		}
		if (!flag) break;
	}
}

例题

1. YBT 1177. 奇数单增序列
2. YBT 1176. 谁考了第 k 名
3. YBT 1178. 成绩排序

哈希初步

在初级阶段哈希的基本思想就是植入下标。

例题 1：有 $N$ 个数（$N\le 10000000$），每一个数的范围是 $[1,1000]$，请输出个数最多的数。

const int N = 1010;
int a[N];

// hash 处理
int n; // 数的总个数
cin >> n;
for(int i = 0; i < n; i++){
	int x;
	cin >> x;
	a[x]++;
}

int ans = -1;
for(int i = 1; i <= N; i++)
	if(ans < a[i]) ans = a[i];

例题 2：有 n 个 1 到 1000 之间的随机整数（n <= 100)，对于其中重复的数字，只保留一个，把其余相同的数去掉后，从小到大排序输出剩下的数。

int a[1010];

for(int i = 0; i < n; i++) {
	int x;
	cin >> x;
	a[x] = 1;
}

for(int i = 1; i <= 1000; i++) {
	if(a[i] == 1) cout << i << " ";
}

例题

1. YBT 1117. 整数去重
2. YBT 1107. 校门外的树

一维数组的例题

首元素问题

将数组的第一个元素移动到数组的末尾，然后所有元素依次往前平移一个位置。

宾馆开关门

宾馆里有 $n(2\le n\le 1000)$ 个房间，从 $1\sim n$ 编了号。第一个服务员把所有的房间门都打开了，第二个服务员把所有编号是 $2$ 的倍数的房间“相反处理”，第三个服务员把所有编号是 $3$ 的倍数的房间作“相反处理”…，以后每个服务员都是如此。当第 $n$ 个服务员来过后，哪几扇门是打开的。（所谓“相反处理”是：原来开着的门关上，原来关上的门打开。）

约瑟夫问题

$n(n<=100)$ 个人围成一个圈，从第一个人开始报数，数到 $m$ 的人出圈，再由下一个人开始报数，数到 $m$ 的人出圈，以此类推，直到所有人出圈，请依次输出出圈人的编号。

#include <iostream>

using namespace std;

const int N = 110;
int a[N];

int main(){
	int n, m;
	cin >> n >> m;
	int f = 0, t = 0, s = 0; // f：出圈的人数 t：圈中的位置 s：实际的人数
	while(f < n) {
		t++;
		if(t == n + 1) t = 1;
		if(a[t] == 0) s++;
		if(s == m) {
			s = 0;
			cout << t << " ";
			a[t] = 1;
			f++;
		}
	}
	cout << endl;

	return 0;
}

数组最大值所处的位置

输入 $n(n<=1000)$ 个整数，输出最大值所处的位置。

数组的数组——二维数组

如果一维数组的元素类型也是一维数组，便构成了“数组的数组”——即二维数组。

示例：二维数组 a

-	第 0 列	第 1 列	第 2 列	第 j 列
第 0 行	a[0, 0]	a[0, 1]	a[0, 2]	a[0, j]
第 1 行	a[1, 0]	a[1, 1]	a[1, 2]	a[1, j]
第 2 行	a[2, 0]	a[2, 1]	a[2, 2]	a[2, j]
第 i 行	a[i, 0]	a[i, 1]	a[i, 2]	a[i, j]

例题 0： 铺地毯

题目描述

为了准备一个独特的颁奖典礼，组织者在会场的一片矩形区域（可看做是平面直角坐标系的第一象限）铺上一些矩形地毯。一共有 $n$ 张地毯，编号从 $1$ 到 $n$。现在将这些地毯按照编号从小到大的顺序平行于坐标轴先后铺设，后铺的地毯覆盖在前面已经铺好的地毯之上。

地毯铺设完成后，组织者想知道覆盖地面某个点的最上面的那张地毯的编号。注意：在矩形地毯边界和四个顶点上的点也算被地毯覆盖。

输入格式

输入共 $n+2$ 行。

第一行，一个整数 $n$，表示总共有 $n$ 张地毯。

接下来的 $n$ 行中，第 $i+1$ 行表示编号 $i$ 的地毯的信息，包含四个整数 $a,b,g,k$，每两个整数之间用一个空格隔开，分别表示铺设地毯的左下角的坐标 $(a,b)$ 以及地毯在 $x$ 轴和 $y$ 轴方向的长度。

第 $n+2$ 行包含两个整数 $x$ 和 $y$，表示所求的地面的点的坐标 $(x,y)$。

输出格式

输出共 $1$ 行，一个整数，表示所求的地毯的编号；若此处没有被地毯覆盖则输出 -1。

样例 #1

样例输入 #1

3
1 0 2 3
0 2 3 3
2 1 3 3
2 2

样例输出 #1

3

样例 #2

样例输入 #2

3
1 0 2 3
0 2 3 3
2 1 3 3
4 5

样例输出 #2

-1

提示

【样例解释 1】

如下图，$1$ 号地毯用实线表示，$2$ 号地毯用虚线表示，$3$ 号用双实线表示，覆盖点 $(2,2)$ 的最上面一张地毯是 $3$ 号地毯。

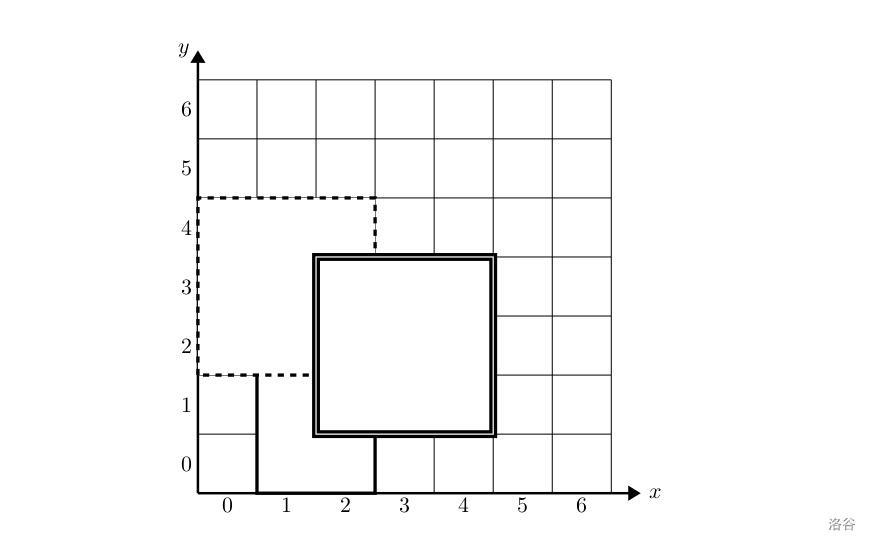
【数据范围】

对于 $30\mathrm{\%}$ 的数据，有 $n\le 2$。
对于 $50\mathrm{\%}$ 的数据，$0\le a,b,g,k\le 100$。
对于 $100\mathrm{\%}$ 的数据，有 $0\le n\le {10}^4$, $0\le a,b,g,k\le {10}^5$。

参考代码

#include <bits/stdc++.h>

using namespace std;

int a[10010][4], n, x, y; // a存储的地毯信息

int main() {
	cin >> n;
	for(int i = 0; i < n; i++) {
		for (int j = 0; j < 4; j++)
			cin >> a[i][j];
		// cin >> a[i][0] >> a[i][1] >> a[i][2] >> a[i][3];
	}
	cin >> x >> y;

	int cur = 0;  // 当前的地毯编号
	int ans = -1;
	for(int i = 0; i < n; i++) {
		cur++;
		int x1 = a[i][0];
		int y1 = a[i][1];		// 地毯左下角的坐标 (x1, y1)
		int x2 = x1 + a[i][2];
		int y2 = y1 + a[i][3];	// 地毯右上角的坐标 (x2, y2)

		if(x >= x1 && x <= x2 && y >= y1 && y <= y2) {
			// 如果坐标(x, y)被地毯覆盖
			ans = cur;
		}
	}

	cout << ans << endl;

	return 0;
}

例题 1：旗鼓相当的对手（多维数组）

题目描述

现有 $N$ 名同学参加了期末考试，并且获得了每名同学的信息：语文、数学、英语成绩（均为不超过 $150$ 的自然数）。如果某对学生 $\text{<}i,j\text{>}$ 的每一科成绩的分差都不大于 $5$，且总分分差不大于 $10$，那么这对学生就是“旗鼓相当的对手”。现在想知道这些同学中，有几对“旗鼓相当的对手”？同样一个人可能会和其他好几名同学结对。

输入格式

第一行一个正整数 $N$。

接下来 $N$ 行，每行三个整数，其中第 $i$ 行表示第 $i$ 名同学的语文、数学、英语成绩。最先读入的同学编号为 $1$。

输出格式

输出一个整数，表示“旗鼓相当的对手”的对数。

样例 #1

样例输入 #1

3
90 90 90
85 95 90
80 100 91

样例输出 #1

2

提示

数据保证，$2\le N\le 1000$ 且每科成绩为不超过 $150$ 的自然数。

参考代码

#include <bits/stdc++.h>

using namespace std;

int s[1010][3], n;

int main() {
	cin >> n;
	for (int i = 0; i < n; i++) {
		cin >> s[i][0] >> s[i][1] >> s[i][2];
	}

	int ans = 0;
	for (int i = 0; i < n; i++) {
		for (int j = i + 1; j < n; j++) {
			int c = abs(s[i][0] - s[j][0]);
			int m = abs(s[i][1] - s[j][1]);
			int e = abs(s[i][2] - s[j][2]);
			int t = abs(s[i][0] + s[i][1] + s[i][2] - s[j][0] - s[j][1] - s[j][2])
			if (c <= 5 && m <= 5 && e <= 5 && t <= 10) ans++;
		}
	}

	cout << ans << endl;

	return 0;
}

例题 2：彩票摇奖

题目描述

为了丰富人民群众的生活、支持某些社会公益事业，北塔市设置了一项彩票。该彩票的规则是：

1. 每张彩票上印有 $7$ 个各不相同的号码，且这些号码的取值范围为 $1\sim 33$。
2. 每次在兑奖前都会公布一个由七个各不相同的号码构成的中奖号码。
3. 共设置 $7$ 个奖项，特等奖和一等奖至六等奖。

兑奖规则如下：

• 特等奖：要求彩票上 $7$ 个号码都出现在中奖号码中。
• 一等奖：要求彩票上有 $6$ 个号码出现在中奖号码中。
• 二等奖：要求彩票上有 $5$ 个号码出现在中奖号码中。
• 三等奖：要求彩票上有 $4$ 个号码出现在中奖号码中。
• 四等奖：要求彩票上有 $3$ 个号码出现在中奖号码中。
• 五等奖：要求彩票上有 $2$ 个号码出现在中奖号码中。
• 六等奖：要求彩票上有 $1$ 个号码出现在中奖号码中。

注：兑奖时并不考虑彩票上的号码和中奖号码中的各个号码出现的位置。例如，中奖号码为 $2331114191718$，则彩票 $1289231167$ 由于其中有两个号码（$23$ 和 $1$）出现在中奖号码中，所以该彩票中了五等奖。

现已知中奖号码和小明买的若干张彩票的号码，请你写一个程序帮助小明判断他买的彩票的中奖情况。

输入格式

输入的第一行只有一个自然数 $n$，表示小明买的彩票张数；

第二行存放了 $7$ 个介于 $1$ 和 $33$ 之间的自然数，表示中奖号码；

在随后的 $n$ 行中每行都有 $7$ 个介于 $1$ 和 $33$ 之间的自然数，分别表示小明所买的 $n$ 张彩票。

输出格式

依次输出小明所买的彩票的中奖情况（中奖的张数），首先输出特等奖的中奖张数，然后依次输出一等奖至六等奖的中奖张数。

样例 #1

样例输入 #1

2
23 31 1 14 19 17 18
12 8 9 23 1 16 7
11 7 10 21 2 9 31

样例输出 #1

0 0 0 0 0 1 1

提示

数据规模与约定

对于 $100\mathrm{\%}$ 的数据，保证 $1\le n<1000$。

参考代码

#include <bits/stdc++.h>

using namespace std;

// s 存储小明买的每一张彩票
// a[i][0] 存储中奖号码 a[i][1] 存储这个号码被计数了吗
// p 统计每一级别奖的数目 特等奖是 p[7] 六等奖是 p[1]
int s[1010][7], n, a[7][2], p[8];

int main() {
	cin >> n;
	for (int i = 0; i < 7; i++) {
		cin >> a[i][0];
	}
	for (int i = 0; i < n; i++) {
		for (int j = 0; j < 7; j++) {
			cin >> s[i][j];
		}
	}

	for (int i = 0; i < n; i++) {
		int cnt = 0; // 记录彩票号码中有多少个是中奖号码
		for (int j = 0; j < 7; j++) {
			a[j][1] = 0; // 清理兑奖痕迹
		}
		// 开始模拟兑奖
		for (int j = 0; j < 7; j++) { // 小明的 7 个号码
			for (int k = 0; k < 7; k++) { // 中奖号码
				if (a[k][1] == 0 && s[i][j] == a[k][0]) {
					// 中奖号码没被用过且和小明的号码一致
					cnt++;
					a[k][1] = 1;
				}
			}
		}
		// 统计奖项数量
		p[cnt]++;
	}

	for (int i = 8 - 1; i > 0; i--) {
		cout << p[i] << " ";
	}
	cout << endl;

	return 0;
}

YBT 1126：矩阵转置

将一个$n$ 行 $m$ 列矩阵的行、列数据互换后输出。（$1\le n\le 100，1\le m\le 100$）

【输入数据】

3 3
1 2 3
4 5 6
7 8 9

【输出数据】

1 4 7
2 5 8
3 6 9

#include<bits/stdc++.h>

using namespace std;

const int N = 110;
int a[N][N], n, m;

int main() {
    cin >> n >> m;
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            cin >> a[i][j];
        }
    }
   
	// 转置之后变成了 m 行 n 列
    for (int i = 0; i < m; i++) {
        for (int j = 0; j < n; j++) {
            cout << a[j][i] << " ";
        }
        cout << endl;
    }

    return 0;
}

YBT 1127：图像旋转

输入一个 $n$ 行 $m$ 列的黑白图像，将它顺时针旋转 90 度后输出。（$1\le n\le 100，1\le m\le 100$）

【输入数据】

3 3
1 2 3
4 5 6
7 8 9

【输出数据】

7 4 1
8 5 2
9 6 3

【参考代码】(行变列，逆序；列变行，正序)

#include<bits/stdc++.h>

using namespace std;

const int N = 110;
int a[N][N], n, m;

int main() {
    cin >> n >> m;
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            cin >> a[i][j];
        }
    }

	// 旋转90度后矩阵变成了 m 行 n 列
    for (int i = 0; i < m; i++) {
	    // 每行倒着输出
        for (int j = n - 1; j >= 0; j--) {
            cout << a[j][i] << " ";
        }
        cout << endl;
    }
   
    return 0;
}

！思考：

1. 如果逆时针旋转 90 度呢? (行变列，正序；列变行、逆序)
2. 顺时针旋转 180 度呢？（行变行、逆序；列变列、逆序）

对角线问题

一个 $n$ 行 $m$ 列的矩阵（下标从 1 开始），以 $(x,y)$ 点为基准构建对角线，对角线上的元素值都加上 $c$，输出修改后的矩阵。（$x\le n\le 100,y\le m\le 100$）

【输入数据】

5 5
5 8 5 4 2
6 8 9 10 3
10 23 5 2 4
5 9 26 8 23
6 5 8 9 11
2 4 10

【输出数据】

5 8 15 4 12
6 8 9 20 3
10 23 15 2 14
5 19 26 8 23
16 5 8 9 11

【参考代码】

#include<bits/stdc++.h>

using namespace std;

const int N = 110;
int a[N][N], n, m, x, y, c;

int main() {
    cin >> n >> m;
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            cin >> a[i][j];
        }
    }

    cin >> x >> y >> c;
    // 正对角线，左下到右上：i + j == x + y
    // 反对角线，左上到右下：i - j == x - y || j - i == y - x
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            if (i + j == x + y || i - j == x - y) {
                cout << a[i][j] + c << " ";
            } else {
                cout << a[i][j] << " ";
            }
        }
        cout << endl;
    }

    return 0;
}

习题 YBT 2041：【例 5.9】新矩阵

YBT 2042：【例 5.10】稀疏矩阵

【参考代码】

#include<bits/stdc++.h>

using namespace std;

int n, m;

int main() {
    cin >> n >> m;
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
	        int t; cin >> t;
            if (t) {
                cout << i << " " << j << " " << t << endl;
            }
        }
    }

    return 0;
}

YBT 2043：【例 5.11】杨辉三角形

打印杨辉三角形的前 $n$ ($2\le n\le 20$)行。

【输入数据】

5

【输出数据】

1
1 1
1 2 1
1 3 3 1
1 4 6 4 1

【参考代码】

#include<bits/stdc++.h>

using namespace std;

const int N = 25;
int a[N][N];

int main() {
    int n; cin >> n;
    a[1][1] = 1;

    for (int i = 2; i <= n; i++) { // 行
        for (int j = 1; j <= i; j++) {
	        // 关键代码
            a[i][j] = a[i - 1][j - 1] + a[i - 1][j];
        }
    }

    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= i; j++) {
            cout << a[i][j] << " ";
        }
        cout << endl;
    }

    return 0;
}

YBT 2045：【例 5.13】蛇形填数

【参考代码】

#include<bits/stdc++.h>

using namespace std;

const int N = 25;
int a[N][N];
int dx[] = {1, 0, -1, 0};
int dy[] = {0, -1, 0, 1};

int main() {
    int n; cin >> n;
    int i = 1, x = 1, y = n, d = 0; // d 初始方向 0 向下 1 左 2 上 3 右

    while (i <= n * n) {
        a[x][y] = i++;
        int sx = x + dx[d], sy = y + dy[d];
        if (a[sx][sy] || sx > n || sx < 1 || sy > n || sy < 1) {
            // 下标越界 变换方向
            d = (d + 1) % 4;
        }
        x += dx[d], y += dy[d];
    }


    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= n; j++) {
            cout << a[i][j] << " ";
        }
        cout << endl;
    }

    return 0;
}

奇数幻方

奇数幻方指的是一个 $N\ast N$ （$N$ 是奇数）大小的数字矩阵，它的每一行、每一列和两条对角线上的数字之和都相等。

构造方式：