程序的基本结构

在正式上课之前，我们给大家出一道思考题，以来检验同学们对上节课变量模块的学习成果如何？问题是这样的：我们知道如果需要交换两个变量的值，一般情况下我们会借助第三个变量来做，代码如下：

int a = 9, b = 12;

// 交换a b
int t = a;
a = b;
b = t;

现在请大家思考：在不借助第三个变量的情况下，如何交换$a,b$的值？

解析：

a = a + b; b = a - b; a = a - b;

在 C++中有三大程序结构，分别是顺序结构、分支结构和循环结构。它们是构建高楼大厦（复杂程序）的框架结构！

顺序结构

顺序结构没什么好说的，它是自上而下，依次执行每一条语句，直到结束。迄今为止，我们写的所有代码都是顺序结构的。顺序结构的流程图如下：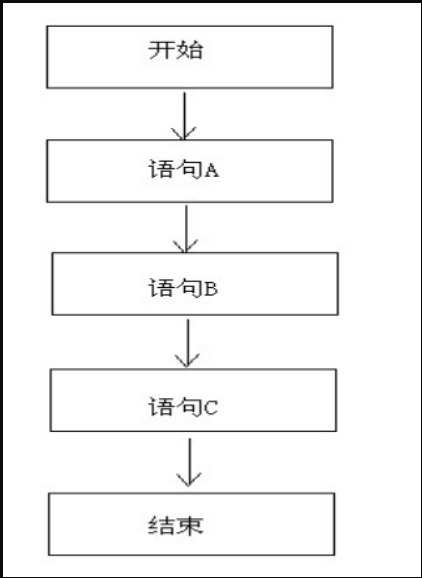

例题

反转三位数

输入一个三位正整数，请反转它。例如：输入123输出321，输入300输出3。

#include <iostream>
#include <cstdio>

using namespace std;

int main(){
	int n; cin >> n;
	int a, b, c; // 个 十 百

	a = n % 10;
	b = n / 10 % 10;
	c = n / 10 / 10 % 10;

	int ans = c + b * 10 + a * 100;

	cout << ans << endl;

	return 0;
}

平均分

已知某班有男同学 $x$ 位，女同学 $y$ 位，$x$ 位男生平均分是 87 分，$y$ 位女生的平均分是 85， 问全体同学平均分是多少分？

分析：平均成绩为：$\frac{(x\ast 87+y\ast 85)}{(x+y)}$

#include <iostream>
#include <cstdio>

using namespace std;

int main(){
	int x, y;
	cin >> x >> y;

	double ans = double(x * 87 + y * 85) / (x + y);
	// 下面这行是错误的
	// double ans = (x * 87 + y * 85) / (x + y);

	cout << ans << endl;

	return 0;
}

平均分 2

歌手大奖赛上 6 名评委给一位参赛者打分，6 个人打分的平均分为 9.6 分；如果去掉一个最高分，这名参赛者的平均分为 9.4 分；如果去掉一个最低分，这名参赛者的平均分为 9.8 分；如果去掉一个最高分和一个最低分，这名参赛者的平均是多少？

分析：首先求出 6 名评委的总分，然后根据去掉最高分的总分和最低分的总分，求出最高分的分值和最低分的分值，最后总分减去最高分和最低分除以 4 即是答案。

#include <iostream>
#include <cstdio>

using namespace std;

int main(){
	float high, low, all, h_all, l_all, ans;

	all = 6 * 9.6;
	h_all = 5 * 9.4;
	l_all = 5 * 9.8;

	high = all - h_all;
	low = all - l_all;

	ans = (all - high - low) / 4;

	printf("%5.2f\n", ans);
	cout << ans << endl;

	return 0;
}

海伦公式

传说古代的叙拉古国王海伦二世发现的公式，利用三角形的三条边长来求取三角形面积。 已知 △ABC 中的三边长分别为 a,b,c，求 △ABC 的面积。

提示：海伦公式 $s=\sqrt{p\ast (p-a)\ast (p-b)\ast (p-c)}$，其中$p=\frac{(a+b+c)}{2}$

#include <iostream>
#include <cstdio>
#include <cmath>

using namespace std;

int main(){
	float a, b, c;
	scanf("%f%f%f", &a, &b, &c);

	float p = (a + b + c) / 2;
	float s = sqrt(p * (p - a) * (p - b) * (p - c));

	printf("%0.3f\n", s);

	return 0;
}

分钱游戏

分钱游戏。甲、乙、丙三人共有 24 元钱，先由甲分钱给乙、丙两人，所分给的数与各人已有数相同；接着由乙分给甲、丙，分法同前；再由丙分钱给甲、乙，分法亦同前。经上述 三次分钱之后，每个人的钱数恰好一样多。 求原先各人的钱数分别是多少?

分析：设甲乙丙三人的钱分别为a、b、c，由最后的结果倒推。

#include <iostream>
#include <cstdio>
#include <cmath>

using namespace std;

int main(){
	int a, b, c;
	// 最后平分钱数
	a = 8; b = 8; c = 8;

	// 丙分钱给甲乙之前
	a = a / 2; b = b / 2; c = a + b + c;

	// 乙分钱给甲丙之前
	a = a / 2; c = c / 2; b = a + b + c;

	// 甲分钱给乙丙之前
	b = b / 2; c = c / 2; a = a + b + c;

	cout << "a = " << a << " b = " << b << " c = " << c << endl;

	return 0;
}

习题

1. YBT 1031. 反向输出一个三位数
2. YBT 1032. 大象喝水
3. YBT 1036. A * B 问题
4. YBT 1037. 计算 2 的幂
5. YBT 1038. 苹果和虫子

分支（选择）结构

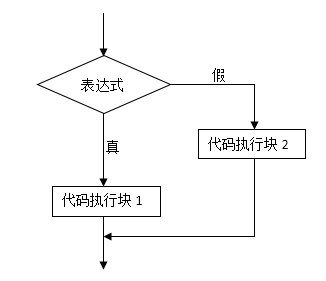
在正式学习分支结构之前，我们需要考虑图中的表达式是什么？由图可知：这里的表达式是可以返回一个布尔值的（即真或假），在 C++中由关系运算符和逻辑运算符构成的条件表达式是可以返回布尔值的（条件成立时返回true，否则返回false）。下面我们来学习这两种运算符。

关系运算符

下表显示了 C++ 支持的关系运算符。

int A = 10, B = 20;

运算符	描述	实例
==	检查两个操作数的值是否相等，如果相等则条件为真。	(A == B) 不为真。
!=	检查两个操作数的值是否相等，如果不相等则条件为真。	(A != B) 为真。
>	检查左操作数的值是否大于右操作数的值，如果是则条件为真。	(A > B) 不为真。
<	检查左操作数的值是否小于右操作数的值，如果是则条件为真。	(A < B) 为真。
>=	检查左操作数的值是否大于或等于右操作数的值，如果是则条件为真。	(A >= B) 不为真。
<=	检查左操作数的值是否小于或等于右操作数的值，如果是则条件为真。	(A <= B) 为真。

逻辑运算符

下表显示了 C++ 支持的关系逻辑运算符。

int A = 1, B = 0;

运算符	描述	实例
&&	称为逻辑与运算符。如果两个操作数都 true，则条件为 true。	(A && B) 为 false。
||	称为逻辑或运算符。如果两个操作数中有任意一个 true，则条件为 true。	(A || B) 为 true。
!	称为逻辑非运算符。用来逆转操作数的逻辑状态，如果条件为 true 则逻辑非运算符将使其为 false。	!(A && B) 为 true。

注意： 这两类运算符构成的表达式是会返回值的，其返回值为 true 或 false。

注意： 这两类运算符的优先级请参见上一章

if 语句

if 单分支

格式：

if (条件表达式) {
    语句1;
    语句2;
    ...
}

解释：如果条件表达式为真则执行花括号里的语句，否则什么也不做。

大括号括起来的语句被称为复合语句或是语句块。如果条件满足时只需要执行一条语句，则大括号也可以省略。

注意代码风格！

• 思考：输入三个数，按照从大到小的顺序输出。我们现在只允许使用 if 单分支

int a, b, c;
cin >> a >> b >> c;
int t;
if (a < b) {
	t = a;
	a = b;
	b = t;
}
if (a < c) {
	t = a;
	a = c;
	c = t;
}
if (b < c) {
	t = b;
	b = c;
	c = t;
}

if...else...双分支

格式：

if (条件表达式) {
    语句1;
    语句2;
    ...
} else {
    语句1;
    语句2;
    ...
}

解释：如果条件表达式为真则执行if后花括号里的语句，否则执行else后花括号里的语句。

• 例题：输入温度 t，判断其是否适合晨练。（$25<=t<=30$，适合晨练（YES），否则不适合晨练（NO））

  int main() {
  	int t; cin >> t;
  	if (t >= 25 && t <= 30) cout << "YES" << endl;
  	else cout << "NO" << endl;
  
  	return 0;
  }

提示：

简单的双分支结构可以使用条件运算符代替

a ? b : c;

语义：如果条件 a 成立则执行 b，否则执行 c。

例子： int a = 3 > 4 ? 3 : 4，结果 a = 4

if 嵌套（多分支）

if 语句是可以嵌套使用的，就像下面这种情况：

if () {
	if () {

	}
}
// if else
if () {
	if () {

	}
} else {
	if () {

	} else {

	}
}

其中我们使用最多的一种嵌套就是 if...else...与 if...else...嵌套，为此 C++提供了 if...else if...else...多分支结构。

格式：

if (条件表达式1) {
    语句1;
    语句2;
    ...
} else if (条件表达式2) {
    语句1;
    语句2;
    ...
} else {
    语句1;
    语句2;
    ...
}

解释：如果条件表达式 1 成立则执行其后的语句块，否则去看条件表达式 2，如果条件表达式 2 成立，则执行其后的语句块，否则（也就是条件表达式 1、2 都不成立）执行 else 后的语句块

• 例题 如果一个年份能被 4 整除且不能被 100 整除；或者年份能被 400 整除，则它就是闰年。输入一个年份，判断是否是闰年

  int main() {
  	int year; cin >> year;
  
  	if ((year % 4 == 0 && year % 100 != 0) || (year % 400 == 0)) {
  		cout << "Yes" << endl;
  	} else {
  		cout << "No" << endl;
  	}
  
  	return 0;
  }

• 思考：输出三个数中的最大值。

  if (a > b && a > c) {
  	cout << a << endl;
  } else if (b > a && b > c) {
  	cout << b << endl;
  } else {
  	cout << c << endl;
  }

习题

1. YBT 1047. 判断能否被 3、5、7 整除
2. YBT 1051. 分段函数

switch 语句（多分支）

格式：

switch(表达式) {
    case 常量表达式1:
        语句1;
        break;
    case 常量表达式2:
        语句2;
        break;
    case 常量表达式n - 1:
        语句n - 1;
        break;
    default:
        语句n;
}

语句执行过程：

1. 计算出 switch 括号中表达式的值，要求为整型。
2. 找到对应的常量表达式的值，执行后面的代码。
3. 开始执行，直到遇到 break 退出

注意事项：

1. 表达式和常量表达式的值都应该是整型，或是能强制转换为整型。
2. case 后面的常量表达式的值不能出错，否则会出错。
3. case 与 default 后面如有多条语句，不需要用花括号。
4. default 可以省略，末尾也不需要 break。
5. 如果没有遇到 break，程序会一直执行下去，直到遇到 break。

• 例子：思考当输入 1，2，3，4 时的输出结果

  int main() {
  	int n; cin >> n;
  
  	switch (n) {
  		case 0: {
  			cout << "0" << endl;
  		}
  		case 1: {
  			cout << "1" << endl;
  			break;
  		}
  		case 2: {
  			cout << "2" << endl;
  		}
  		case 3: {
  			cout << "3" << endl;
  			break;
  		}
  		default: {
  			cout << "unknown" << endl;
  			// break;
  		}
  	}
  
  	return 0;
  }

习题

1. YBT 1049. 晶晶赴约会
2. YBT 1050. 骑车与走路
3. YBT 1052. 计算邮资
4. YBT 1056. 点和正方形的关系
5. YBT 1057. 简单计算器

循环结构

循环结构的本质也是顺序结构，它只是将具有相同功能的代码有效的组织在一起，循环执行。

为什么需要循环呢？

编写少量的代码，执行大量重复的工作！

引例

请输出数字1 到 10。

利用之前学过的顺序结构的知识我们可以使用十条cout语句解决这道题，但是如果要求输出1 到一万呢？或者更多呢？有没有更好的方式呢？我们知道这是一个重复的事情，只不过第一次重复输出的是 1，而第二次重复输出的是 2，以此类推而已。那我们能不能想出一个方法来完成这件事呢？

让变量 i 从 1 变到 10000:
	每一次变化输出变量 i

上面我们描述的过程即是循环！重复的事情使用循环。从上面的循环描述中我们可以看到循环的三要素：

1. 循环变量
2. 终止条件
3. 增量表达式

for 循环

格式：

for (循环变量初始化; 条件表达式; 增量表达式) {
    // 循环体
    语句1;
    语句2;
    ...
    语句n;
}

• 循环体是一个复合语句，也可以是单条语句。

执行过程：for 中分 3 个部分，第 1 个部分的循环变量初始化只执行 1 次

1. 循环变量初始化，使循环变量获得初始值。
2. 判断条件表达式是否成立，如果成立，则执行一遍循环体；如果不成立，则结束整个循环。
3. 对循环变量增量，使其获得新值。
4. 自动转到第 2 步执行，直到整个循环结束。

示例：计算 1 + 2 + 3 + ... + 100

int sum = 0;
for (int i = 1; i <= 100; i++) {
	sum += i
}

cout << sum << endl;
// 下面这行会报错，因为i是一个for语句中的局部变量
// cout << i << endl;

注意：循环变量是一个局部变量，如上例，如果在循环外访问i变量则会报编译错误！

提示：for 循环的格式很灵活，它的三个部分都可以省略

// 1 在for循环中省略循环变量初始化
int i = 1; // 循环变量初始化写在for循环外面
for (; i <= 100; i++) sum += i;
// 下面这行语句不会报错
// cout << i << endl;

// 2
int i = 1;
for (; i <= 100; ) {
	sum += i;
	i++;
}

// 3
int i = 1;
for (; ;) {
	if (i > 100) break;
	sum += i;
	i++;
}

循环控制：break 和 continue

break：跳出整个循环

continue：跳出本层循环，继续下一层循环

for (int i = 1; i <= 10; i++) {
	if (i == 5) break;
	cout << i << endl;
}

for (int i = 1; i <= 10; i++) {
	if (i == 5) continue;
	cout << i << endl;
}

求和

求 1 到 100 中的奇数和和偶数和。

int main() {
	int sum1 = 0, sum2 = 0; // sum1奇数和 sum2偶数和
	for (int i = 1; i <= 100; i++) {
		if (i % 2 != 0) sum1 += i;
		else sum2 += i;
	}

	cout << sum1 << " " << sum2 << endl;

	return 0;
}

求 n 的阶乘

求 $n!$。 $n!=1\ast 2\ast 3\ast 4\ast ...\ast n$。

int main() {
	int n; cin >> n;

	int ans = 1;
	for (int i = 1; i <= n; i++) {
		ans *= i;
	}

	cout << ans << endl;

	return 0;
}

求 n 个数中的最大值

输入 n 个数， 输出这 n 个数中的最大值。

int main() {
	int n; cin >> n;

	int ans = -1e9;
	for (int i = 0; i < n; i++) {
		int t; cin >> t;
		ans = max(ans, t);
	}

	cout << ans << endl;

	return 0;
}

求整数的和与均值

输入 n 个整数， 输出它们的和与平均值（保留两位小数）

int main() {
	int n; scanf("%d", &n);

	int sum = 0;
	double avg = 0.0;

	for (int i = 0; i < n; i++) {
		int t; scanf("%d", &t);
		sum += t;
	}

	printf("%d %.2lf\n", sum, sum / (double)n);

	return 0;
}

一道有趣的思考题？

• 时空限制： 1s 64MB

【题目描述】

  在股市中买卖股票通常是这样的：在股价低的时候买入，在股价高的时候卖出。需要注意的是你不能在今日买入的同时又卖出它。因为我们精力有限，所以我们只能操纵一支股票。一旦进入股市，就无法回头了，所以为了保险你打算试试手：选择一支股票，无论亏损还是盈利，只买卖一次！

  现在给出目标股票在一段时期（$n$日）内的每一日 $t$ 的价格 $R_t(t=0,1,2,3...n-1)$，请计算你的最大获利（或是最小的亏损）。

【输入描述】

第 1 行输入整数 $n$。接下来 $n$ 行依次给出整数 $R_t(t=0,1,2,3...n-1)$

【输出描述】

最大获利

【示例 1】

输入：

6
7 1 5 3 6 4

输出：

5

解释：

在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大获利 = 6 - 1 = 5 。注意获利不能是 7 - 1 = 6, 因为卖出价格需要大于买入价格；同时，你不能在买入前卖出股票。

【示例 2】

输入：

5
7 6 4 3 1

输出：

-1

解释：

由于我们必须买卖一次，所以在最小的亏损为 -1

【限制 1】

$2\le n\le 2000$

$1\le R_t\le {10}^9$

【限制 2】

$2\le n\le 200000$

$1\le R_t\le {10}^9$

#include <bits/stdc++.h>

using namespace std;

int main() {
	int a[200010];

	int n; cin >> n;
	for (int i = 0; i < n; i++) {
		cin >> a[i];
	}

	int ans = -2e9 + 10;
	for (int i = 0; i < n; i++) {
		for (int j = i + 1; j < n; j++) {
			ans = max(ans, a[j] - a[i]);
		}
	}

	cout << ans << endl;

	return 0;
}

// 2
#include <bits/stdc++.h>

using namespace std;

int main() {
	int n; cin >> n;

	int ans = -2e9 + 10, minv;
	cin >> minv;

	for (int i = 1; i < n; i++) {
		int t; cin >> t;
		ans = max(ans, t - minv);
		minv = min(minv, t);
	}

	cout << ans << endl;

	return 0;
}

习题

1. YBT 1059. 求平均年龄
2. YBT 1061. 求整数的和与均值
3. YBT 1062. 最高的分数
4. YBT 1064. 奥运奖牌计数
5. YBT 1065. 奇数求和
6. YBT 1068. 与指定数字相同的数的个数
7. YBT 1069. 乘方计算
8. YBT 1071. 菲波那契数
9. YBT 1072. 鸡尾酒疗法
10. YBT 1074. 津津的储蓄计划
11. YBT 1077. 统计满足条件的 4 位数
12. YBT 1079. 计算分数加减表达式的值

while 循环

格式：

while (条件表达式) {
    循环体
}

while 循环需要具备循环的三要素，否则容易写成死循环。

示例：计算 1 + 2 + 3 + ... + 100

int sum = 0, i = 1;
while(i <= 100) {
	sum += i;
	i++;
}
cout << sum << endl;

• 为什么会有while循环呢？for循环不够用吗？下面我们给出这个问题的一种回答，请考虑下面的问题。

满足条件的 n 值

求满足不等式 $1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+...+\frac{1}{n}\ge 5$ 的最小 $n$ 值。

分析

我们在这里能使用for循环吗？当然可以，不过是比较麻烦的，同学们可以思考一下。那么我们使用while循环呢？试着写一下代码？

int s = 0, i = 1;
while (s < 5) {
	s += 1.0 / i;
	i++;
}

是不是很简单明了？不是吗？现在知道为什么使用while循环了吗？

我们知道for循环更适用于已知循环次数的情况，而在不确定循环多少次时，请考虑使用while循环！

最大公约数

求整数 $m$ 和 $n$ 的最大公约数。

分析

我们通常使用 $gcd(a,b)$ 表示 $a,b$ 的最大公约数，而 $lcm(a,b)$ 则用来表示 $a,b$ 的最小公倍数。我们知道 $a\ast b=gcd(a,b)\ast lcm(a,b)$，利用欧几里得算法（辗转相除法）知 $gcd(a,b)=gcd(b,a\mathrm{\%}b)$ 当 $a\mathrm{\%}b==0$ 时 $b$ 即为所求最大公约数

证明

引理：若 $a=bq+r$，其中 $a,b,q,r$ 均为整数，且 $0\le r<b$，那么 $gcd(a,b)=gcd(b,r)$。

证明：

设 $d=gcd(a,b)$，则 $d|a$，$d|b$。

由 $r=a-bq$，知 $d|r$。

因此 $d$ 是 $b$ 和 $r$ 的一个公约数。

设 $d^{\prime }=gcd(b,r)$，则 $d^{\prime }|b$，$d^{\prime }|r$。

由 $a=bq+r$，知 $d^{\prime }|a$。

因此 $d^{\prime }$ 是 $b$ 和 $r$ 的另一个公约数。

由于 $d$ 是 $a,b$ 的最大公约数，所以 $d^{\prime }|d$。

由于 $d^{\prime }$ 是 $b,r$ 的最大公约数，而 $d$ 是 $b,r$ 的一个公约数，所以 $d|d^{\prime }$。

于是 $d^{\prime }=d$，因此 $gcd(a,b)=gcd(b,r)$。

while (a % b) {
	int t = b;
	b = a % b;
	a = t;
}

数据统计

输入一些整数，求出它们的最小值、最大值和平均值（保留 3 位小数）。输入保证这些数都是不超过 1000 的整数。

分析

因为这道题没有告诉我们确切输入几个数，那么我们如何读入呢？使用scanf或是cin的返回值来判断读入是否结束！

scanf的返回值是它读取到的数据的个数，如果它读不到任何数据将返回 -1，所以我们可以这样写来判断读入是否结束while (scanf(%d", &x) != -1)

cin在读取不到数据时返回的是 0，也就是说cin在成功读入时返回true，否则返回false，所以我们可以这样写来判断读入是否结束while (cin >> x)

• 注意：本地运行时如果想要结束输入，请先按下回车，再按下Ctrl + Z，最后再按下回车，输入就会结束。

习题

1. YBT 1085. 球弹跳高度的计算
2. YBT 1086. 角谷猜想
3. YBT 1087. 级数求和

do while 循环

  do while 和 while 几乎一样。while 是先判断条件再执行循环体，do while 是先执行一遍循环体再判断条件。因此用 do while 循环体至少被执行一次。

格式：

do {
    循环体
}
while (条件表达式);

一些说明

  在do while循环中也可以使用break和continue，它也满足循环的三要素。为什么会有do while循环呢？一个可能的解释是可能有这样一种情况，无论循环条件是否满足，我都需要一遍循环体！当然了，do while循环能做的while循环和for循环也能做，反之亦然。

习题

1. YBT 2024. 末两位数
2. YBT 2025. 体操队

循环嵌套

循环语句是可以互相嵌套的，甚至可以多层嵌套，而嵌套循环的执行流程很简单：先内而外。下面看一个例子：

打印图形

请打印如下图形：

******
******
******
******
******

分析 我们观察图形有 5 行，每行有 6 个*，那么我们可以for循环解决这道题，代码可能写成这样:

for (int i = 1; i <= 5; i++) {
 	cout << "******" <<endl;
}

还记得一句话吗？重复的事情用循环。我们发现在输出每一行的*的时候，它也是一个循环，那我们可以考虑把cout << "******" << endl;这行代码也改写成循环，试着改写一下：

for (int i = 1; i <= 5; i++) {
	for (int j = 1; j <= 6; j++) {
		cout << "*" << endl;
	}
}

这就是for循环的嵌套，其他循环语句也是如此，它们还可以互相嵌套，多层嵌套。为了加深同学们的认识，请模拟如下代码，写出输出结果。

for (int i = 1; i <= 10; i++) {
	for (int j = 1; j <= 5; j++) {
		cout << i << " " << j << endl;
	}
}

  对于打印图形这道题，可能有的同学说，我一层循环就能解决而且代码还那么简洁，为什么非要写那么多循环，多此一举！那么请同学们使用一层循环打印如下的图形试一试？

*
**
***
****
*****

  此时，我们使用一层循环还容易解决吗？这个时候请考虑使用循环嵌套，并注意i和j（即行和列）的关系

再看打印图形

请打印如下图形

   *
  ***
 *****
*******

    *
   **
  ***
 ****
*****

*******
 *****
  ***
   *

*******
 *****
  ***
   *
  ***
 *****
*******

   *
  ***
 *****
*******
 *****
  ***
   *

素数问题

给出两个整数 $a,ba\le b$ 请输出 $[a,b]$ 中的所有素数（质数）

#include <bits/stdc++.h>

using namespace std;

int main() {
	int a, b;
	cin >> a >> b;

	for (int i = a; i <= b; i++) {
		int t = sqrt(i), j = 2;
		for (j; j <= t; j++) {
			if (i % j == 0) break;
		}
		if (j > t) cout << i << endl;
	}

	return 0;
}

分解质因数

把一个合数分解成若干个质因数乘积的形式(即求质因数的过程)叫做分解质因数。分解质因数(也称分解素因数)只针对合数。

输入一个正整数 $n$，将 $n$ 分解成质因数乘积的形式。

#include <bits/stdc++.h>

using namespace std;

int main() {
	int n; cin >> n;

	cout << n << "=";
	int i = 2;
	while (n != 1) {
		while (n % i == 0) {
			cout << i;
			n /= i;
			if (n != 1) cout << "*";
		}
		i++;
	}

	return 0;
}

数学原理

算术基本定理：任何大于 $1$ 的整数都可以唯一地分解成有限个质数的乘积。

算法实现思路：

从最小的质数 $i=2$ 开始，尝试能否整除当前的 $n$：

1. 如果能整除，说明 $i$ 是 $n$ 的一个质因子，输出 $i$ 并将 $n$ 除以 $i$。
2. 重复步骤 1，直到 $n$ 不能被 $i$ 整除，$i$ 自增 $1$，继续尝试。

关键点：

1. 为什么不回输出合数？

如果 $i$ 是合数，那么它一定有一个质因子 $p<i$，而 $p$ 已经在之前的循环中被试过了，并且把 $n$ 中所有 $p$ 的因子去除了，所以 $n$ 不可能再被 $i$ 整除，因此，实际上进入内层循环的 $i$ 一定是质数。

优化：

枚举 $i$ 可能的取值，从 $2$ 开始，直到 $\sqrt{n}$，这样可以避免一些不必要的循环。

因为 $n$ 最多只有一个大于 $\sqrt{n}$ 的质因子。

void divide(int x) {
    for (int i = 2; i <= x / i; i++) {
        if (x % i == 0) {
            int s = 0;
            while (x % i == 0) {
                x /= i;
                s++;
            }
            cout << i << " " << s << endl;
        }
    }
    if (x > 1) cout << x << " " << 1 << endl;
}

剥数问题

给定一个整数 $n1\le n\le {10}^9$ 统计数字 1 出现的次数。如 3121 1 出现了 2 次

int cnt = 0;
while (n) {
	if (n % 10 == 1) cnt++;
	n /= 10;
}
cout << cnt << endl;

百钱百鸡

百钱买百鸡问题。鸡翁一，值钱五，鸡母一，值钱三，鸡雏三，值钱一，百钱买百鸡，问鸡翁、鸡母、鸡雏各几何？

// 枚举每一种情况
for (int i = 0; i <= 100 / 5; i++) {
	for (int j = 0; j <= 100 / 3; j++) {
		for (int k = 0; k <= 100; k++) {  // 鸡雏最多买 min(100, 300) 只
			if (i + j + k == 100 && 15 * i + 9 * j + k == 300) {
				cout << i << " " << j << " " << k << endl;
			}
		}
	}
}

// 优化1
for (int i = 0; i <= 100 / 5; i++) {
	for (int j = 0; j <= 100 / 3; j++) {
		int k = 100 - i - j;
		if (15 * i + 9 * j + k == 300) {
			cout << i << " " << j << " " << k << endl;
		}
	}
}

// 优化2 解方程 i + j + k = 100 与 15i + 9j + k = 300
for (int i = 0; i <= 100 / 5; i++) {
	int j = 25 - 1.75 * i, k = 75 + 0.75 * i;
	if (j >= 0 && i + j + k == 100 && 15 * i + 9 * j + k == 300) {
		// 思考：为什么这里重新判断了方程等式？
		// i j k 是整形，如果j k的计算结果是小数会发生自动截取
		cout << i << " " << j << " " << k << endl;
	}
}

习题

1. YBT 1088. 分离整数的各个数
2. YBT 1089. 数字反转
3. YBT 1090. 含 k 个 3 的数
4. YBT 1091. 求阶乘的和
5. YBT 1094. 与 7 无关的数
6. YBT 1096. 数字统计
7. YBT 1097. 画矩形
8. YBT 1098. 质因数分解
9. YBT 1100. 金币