树链剖分是将树剖分成若干条链的形式,以维护树上路径的信息。
具体来说,将整棵树剖分为若干条链,使它组合成线性结构,然后用其他的数据结构维护信息。
树链剖分有多种形式,如果没有特殊说明,以下所说的树链剖分指的都是重链剖分。
树链剖分通常用来解决以下问题:
- 树上
到 的最短路径上所有节点权值均加上 - 求树上
到 的最短路径上所有节点权值之和 - 以
为根的子树中所有节点权值均加上 - 求以
为根的子树中所有节点权值之和
重链剖分
- 重子节点:表示其子节点中子树最大的子节点。如果有多个子树最大的子节点,取其中任意一个,如果没有子节点,则无重子节点。
- 轻子节点:表示剩余的所有子节点。
- 从某个节点到重子节点的边为重边。
- 从某个节点到轻子节点的边为轻边。
- 若干条首尾衔接的重边构成重链。把落单的节点也看作重链,则整棵树就被剖分成若干条重链。
如图:
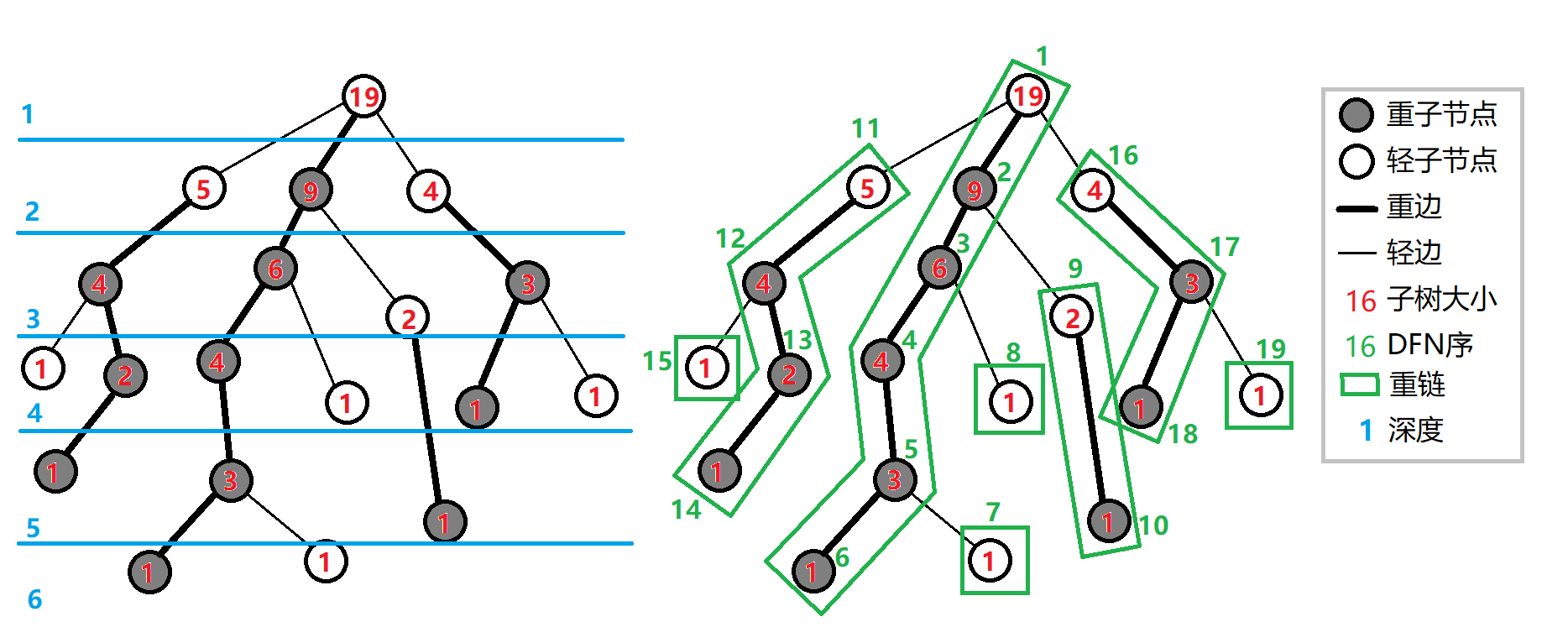
树链剖分的实现
代码实现中需要用到的一些定义:
表示节点 的父亲节点 表示节点 在树上的深度 表示节点 的子树的节点个数 表示节点 的重儿子 表示节点 所在重链的顶部节点 表示节点 的 序,也是其在线段树中的编号 表示 序所对应的节点编号,有
两次
第一次
cpp
void dfs1(int u, int f) {
fa[u] = f, dep[u] = dep[f] + 1, siz[u] = 1;
for (int i = h[u]; i != -1; i = ne[i]) {
int v = e[i];
if (v == f) continue;
dfs1(v, u);
siz[u] += siz[v];
if (siz[v] > siz[son[u]]) son[u] = v;
}
}第二次
cpp
void dfs2(int u, int ftop) {
top[u] = ftop, dfn[u] = ++dfn_cnt, rnk[dfn_cnt] = u;
if (son[u]) dfs2(son[u], ftop); // 存在重儿子则深入
for (int i = h[u]; i != -1; i = ne[i]) {
int v = e[i];
if (v != son[u] && v != fa[u]) dfs2(v, v); // 存在轻儿子则深入
}
}重链剖分的性质:
- 树上每个节点都属于且仅属于一条重链。
- 整棵树会被剖分成若干条重链
- 轻子节点一定是每条重链的顶点
- 在剖分时重边优先遍历,最后树的
序上,重链内的 序是连续的。按 排序后的序列即为剖分后的链。 - 一颗子树内的
序是连续的。 - 任意一条路径被切分成不超过
条链
树链剖分的应用
树链剖分求 LCA
可让节点沿着各自的重链向上跳重链,当跳到同一条重链上时,深度较小的那个节点就是 LCA。
注意:向上跳重链时需要先跳所在重链顶端深度较大的那个。
cpp
int lca(int u, int v) {
while (top[u] != top[v]) {
if (dep[top[u]] < dep[top[v]]) swap(u, v);
u = fa[top[u]];
}
return dep[u] < dep[v]? u : v;
}